RegionDistance
RegionDistance[reg,p]
gives the minimum distance from the point p to the region reg.
RegionDistance[reg]
gives a RegionDistanceFunction[…] that can be applied repeatedly to different points.
Details and Options
- RegionDistance is also known as point-to-region distance, distance transform, distance field and minimum region distance.
- The distance between points q and p is taken to be Norm[p-q].
- Region distance is effectively given by MinValue[{Norm[p-q],q∈reg},q].
- RegionDistance can be used with symbolic regions and points in GeometricScene.
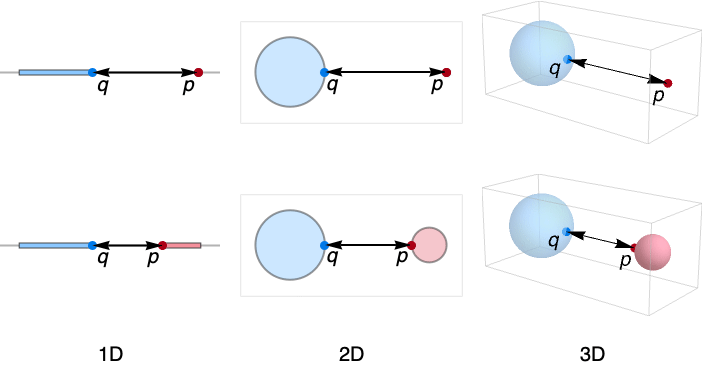
Examples
open allclose allBasic Examples (2)
Find the distance from a point to the unit disk:
Plot the distance as a function of position:
Find the distance from a point to a MeshRegion:
With one argument, you get a RegionDistanceFunction:
Apply the distance function lists of points to compute many distances:
Scope (15)
Special Regions (9)
Formula Regions (2)
The distance to a disk represented as an ImplicitRegion:
The distance to a disk represented as a ParametricRegion:
Mesh Regions (1)
Derived Regions (3)
The distance to a RegionIntersection:
The distance to a TransformedRegion:
The distance to a RegionBoundary:
Applications (5)
Compute the height of a triangle:
Create a region that is a distance 
from a circle:
Visualize the region and circle:
Compute the dilation of a region:
The directed Hausdorff distance from region 
to 
is defined as 
. Use RegionDistance to compute the directed Hausdorff distance from =Triangle[{{0,0},{2,0},{0,1}}] to ℬ=Triangle[{{0,0},{1,0},{0,3/2}}]:
Find the nearest distance to any point in 
:
As expected, the distance is zero for points in 
that overlap with 
:
Find the directed Hausdorff distance by maximizing over 
:
If 
, you can conclude that 
where 
is the closure of 
and 
. Show that 
for the regions in this example:
The Hausdorff distance between region 
and 
is defined as 
where 
is the directed Hausdorff distance in the previous example. Use RegionDistance to compute the Hausdorff distance between =Triangle[{{0,0},{2,0},{0,1}}] and ℬ=Triangle[{{0,0},{1,0},{0,3/2}}]:
Find the directed Hausdorff distances:
If 
, you can conclude that 
and 
, as in the previous example. Show that 
and 
for the regions in this example:
Properties & Relations (4)
A point is a RegionMember if the distance to the region is 0:
RegionDistance is the MinValue of the distance to any point in the region:
RegionNearest gives a point that is of minimal distance from the input:
For a point outside the region, RegionDistance and SignedRegionDistance are the same:
Text
Wolfram Research (2014), RegionDistance, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionDistance.html.
CMS
Wolfram Language. 2014. "RegionDistance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionDistance.html.
APA
Wolfram Language. (2014). RegionDistance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionDistance.html