WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

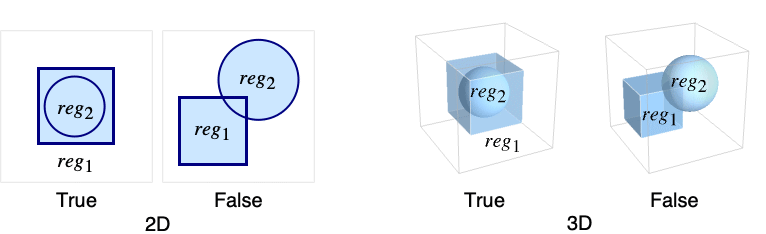
RegionWithin
✖
RegionWithin

✖
RegionWithin[reg1,reg2]

returns True if reg2 is contained within reg1.

Details and Options

  • The region reg2 is contained within reg1 if every point that belongs to reg2 also belongs to reg1.
  • If all regi are parameter-free regions, i.e. ConstantRegionQ[regi] is True, the regions are point sets, and typically True or False is returned.
  • If some regi depend on parameters, i.e. ConstantRegionQ[regi] is False, then regi represents a family of regions, and RegionWithin will attempt to compute conditions on parameters such that reg2 is contained within reg1.
  • The following options can be given:
  • Assumptions $Assumptionsassumptions to make about parameters
    GenerateConditions Falsewhether to generate conditions on parameters

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

Test whether a region is contained within another:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-bwhjpw
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-2rib4
Out[3]=3

Visualize them:

In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-ch8cm5
Out[4]=4

Generate conditions for which a region is contained within another:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-bjcd6
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-bgxf3h
Out[2]=2

Scope  (15)Survey of the scope of standard use cases

Basic Uses  (3)

Test for membership:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-eb93s9
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-firoum
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-gfcy2o
Out[4]=4

Show a region is not within another:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-82vpaa
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-z64t9f
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-30lfif
Out[3]=3

Find conditions that make a region a subset of another:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-tnzyl9
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-w8dsx6
Out[2]=2

Basic Regions  (4)

Regions in including Line and Interval:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-6v3c9q
Out[1]=1

Point:

In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-uiw53u
Out[2]=2

Ball:

In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-0a693w
Out[3]=3

InfiniteLine:

In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-586b1i
Out[4]=4

Regions in including Point:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-i2fp1e
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-fcyt2v
Out[2]=2

Line:

In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-gnymc0
In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-fw05sb
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0i1ptbttm-cpipc8
Out[5]=5

Polygon:

In[6]:=6
✖
https://wolfram.com/xid/0i1ptbttm-45f5fx
In[7]:=7
✖
https://wolfram.com/xid/0i1ptbttm-if4go9
Out[7]=7
In[8]:=8
✖
https://wolfram.com/xid/0i1ptbttm-co6226
Out[8]=8

Disk and Ellipsoid:

In[9]:=9
✖
https://wolfram.com/xid/0i1ptbttm-0aeidt
In[10]:=10
✖
https://wolfram.com/xid/0i1ptbttm-te9loc
Out[10]=10

Rectangle and RegularPolygon:

In[11]:=11
✖
https://wolfram.com/xid/0i1ptbttm-3el84j
Out[11]=11

Regions in including Point:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-ivezrn
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-v4vks4
Out[2]=2

Line:

In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-lm5ega
In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-w3c7x0
Out[4]=4

Polygon:

In[5]:=5
✖
https://wolfram.com/xid/0i1ptbttm-t559ku
In[6]:=6
✖
https://wolfram.com/xid/0i1ptbttm-uaqco4
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0i1ptbttm-pmg8fc
Out[7]=7

Cuboid and Hexahedron:

In[8]:=8
✖
https://wolfram.com/xid/0i1ptbttm-35c0r8
In[9]:=9
✖
https://wolfram.com/xid/0i1ptbttm-g2ry70
Out[9]=9

Ball and Ellipsoid:

In[10]:=10
✖
https://wolfram.com/xid/0i1ptbttm-g1mnn1
In[11]:=11
✖
https://wolfram.com/xid/0i1ptbttm-3j14kp
Out[11]=11

Tetrahedron and Simplex:

In[12]:=12
✖
https://wolfram.com/xid/0i1ptbttm-ilyuwb
In[13]:=13
✖
https://wolfram.com/xid/0i1ptbttm-o1w6u8
Out[13]=13

Regions in including Cuboid and Parallelepiped in :

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-02h4ee
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-29ru1s
Out[2]=2

Ellipsoid and Ball in :

In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-ufst9o
In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-8t7at1
Out[4]=4

Formula Regions  (4)

Implicit regions:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-yhhbit
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-uj1qf1
Out[3]=3

Parametric regions:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-hukmm5
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-jgs1z1
Out[2]=2

Compare two formula regions:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-eie8c4
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-w59lx6
Out[2]=2

Nonconstant formula regions:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-hic6g2
Out[1]=1

Mesh Regions  (3)

Compare MeshRegion in :

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-5yev98
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-ciss1i
Out[3]=3

In :

In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-6p9mf1
In[6]:=6
✖
https://wolfram.com/xid/0i1ptbttm-9eeqmu
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0i1ptbttm-pmpsgg
Out[7]=7

In :

In[8]:=8
✖
https://wolfram.com/xid/0i1ptbttm-ron1r2
In[10]:=10
✖
https://wolfram.com/xid/0i1ptbttm-83vd07
Out[10]=10
In[11]:=11
✖
https://wolfram.com/xid/0i1ptbttm-lz7nun
Out[11]=11

Compare BoundaryMeshRegion in :

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-ki5zz3
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-bt2ml0
Out[2]=2

In :

In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-20k1t
In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-x4jjvo
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0i1ptbttm-d3cir4
Out[5]=5

In :

In[6]:=6
✖
https://wolfram.com/xid/0i1ptbttm-lwhzff
In[7]:=7
✖
https://wolfram.com/xid/0i1ptbttm-tmarje
Out[7]=7
In[8]:=8
✖
https://wolfram.com/xid/0i1ptbttm-2bstik
Out[8]=8

Compare MeshRegion with BoundaryMeshRegion in :

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-eq7jc5
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-n3t5rq
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-w76nww
Out[3]=3

In :

In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-t4fi8f
In[5]:=5
✖
https://wolfram.com/xid/0i1ptbttm-xmhkjc
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0i1ptbttm-vj7fl4
Out[6]=6

Derived Regions  (1)

Compare BooleanRegion:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-pk317t
In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-15qu2j
Out[4]=4

Options  (2)Common values & functionality for each option

Assumptions  (1)

Find all disks that contain the unit circle:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-tajffo
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-raue2j
Out[3]=3

Find only the positive radii:

In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-beh8xv
Out[4]=4

GenerateConditions  (1)

Find when the unit disk lies within an implicitly described annulus:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-y7rzg1
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-2foycc
Out[3]=3

Show the conditions for which the result is valid:

In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-ysjw49
Out[3]=3

Explicitly allow for degenerate cases:

In[5]:=5
✖
https://wolfram.com/xid/0i1ptbttm-cxiwq
Out[5]=5

Applications  (7)Sample problems that can be solved with this function

All convex combinations of points lie within their convex hull:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-c2siwi
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-rvuhoh
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-sg67y4
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-20lr8e
Out[4]=4

Find the largest disk contained in a given triangle:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-5reuia
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-kemxj1
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-r768z0
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-y86c6e
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0i1ptbttm-e2lily
Out[5]=5

Approximate the largest axes-aligned ellipse contained in the triangle:

In[6]:=6
✖
https://wolfram.com/xid/0i1ptbttm-lk1i9r
In[7]:=7
✖
https://wolfram.com/xid/0i1ptbttm-7nzm0f
Out[7]=7
In[8]:=8
✖
https://wolfram.com/xid/0i1ptbttm-nz4gh7
Out[8]=8

Find the smallest disk that contains a given triangle:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-9q21li
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-55wznh
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-7s5d4s
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-vpxmz7
Out[4]=4

Find the smallest axes-aligned ellipse that contains the triangle:

In[5]:=5
✖
https://wolfram.com/xid/0i1ptbttm-mxybiw
In[6]:=6
✖
https://wolfram.com/xid/0i1ptbttm-dtlowt
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0i1ptbttm-ibd3df
Out[7]=7
In[8]:=8
✖
https://wolfram.com/xid/0i1ptbttm-73ihbu
Out[8]=8

Find all countries that lie completely within the Caribbean Sea:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-fpdlyt

The polygons of each country:

In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-4p25ou

Select the countries whose polygons lie within the Caribbean Sea:

In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-s9dghf
Out[3]=3

Verify the results:

In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-g10uxt
Out[4]=4

View these countries on a map:

In[5]:=5
✖
https://wolfram.com/xid/0i1ptbttm-h95zbe
Out[5]=5

Find and visualize all positions where a unit rectangle lies within an annulus:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-59poq7
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-4rztjs
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-xjaxyl
Out[3]=3

Perform a random walk inside a region:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-1eu4a3

Define a function to walk a point in a random direction, staying inside a region:

In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-2t78a9

Simulate a random walk from an initial point:

In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-v10re3
In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-pootx3

Visualize the walk:

In[5]:=5
✖
https://wolfram.com/xid/0i1ptbttm-2vflrc
Out[5]=5

Use RegionWithin as a partial ordering to visualize concentric disks:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-y0dxc3
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-w28qj9

Disks with larger radii can completely cover other disks:

In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-zxfkg6
Out[3]=3

Sort the regions according to membership:

In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-di1dof

Visualize the rearranged disks:

In[5]:=5
✖
https://wolfram.com/xid/0i1ptbttm-0t46az
Out[5]=5

Properties & Relations  (5)Properties of the function, and connections to other functions

Use RegionMember to test the membership of a point:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-vw067z
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-zxr7hs
Out[2]=2

Use RegionWithin to test the membership of a region:

In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-yq8nk9
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-kj9dnc
Out[4]=4

When ℛ2 is within ℛ1, all points in ℛ2 are members of ℛ1:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-ga16k4
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-o48yw3
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-szw6pm
Out[3]=3

Check if two regions are equal:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-fe5guh
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-ej7p5t
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-px5lwy
Out[3]=3

For non‐empty regions, RegionDisjoint returns False when RegionWithin returns True:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-bq0ked
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-foaup4
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-k8st6l
Out[3]=3

Use FindInstance to find points that violate the subset condition:

In[1]:=1
✖
https://wolfram.com/xid/0i1ptbttm-ecv99p
In[2]:=2
✖
https://wolfram.com/xid/0i1ptbttm-i0zv76
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0i1ptbttm-vjwpmf
In[4]:=4
✖
https://wolfram.com/xid/0i1ptbttm-mccqg1
Out[4]=4

Use RandomPoint to find a uniform sampling of points that violate the subset condition:

In[5]:=5
✖
https://wolfram.com/xid/0i1ptbttm-gpkt0l
In[6]:=6
✖
https://wolfram.com/xid/0i1ptbttm-o0kf7b
Out[6]=6

Use Reduce to find where the subset condition is violated:

In[7]:=7
✖
https://wolfram.com/xid/0i1ptbttm-42jril
Out[7]=7
In[8]:=8
✖
https://wolfram.com/xid/0i1ptbttm-ly4r2m
Out[8]=8
Wolfram Research (2017), RegionWithin, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionWithin.html.
✖
Wolfram Research (2017), RegionWithin, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionWithin.html.

Text

Wolfram Research (2017), RegionWithin, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionWithin.html.

✖
Wolfram Research (2017), RegionWithin, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionWithin.html.

CMS

Wolfram Language. 2017. "RegionWithin." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionWithin.html.

✖
Wolfram Language. 2017. "RegionWithin." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionWithin.html.

APA

Wolfram Language. (2017). RegionWithin. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionWithin.html

✖
Wolfram Language. (2017). RegionWithin. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionWithin.html

BibTeX

@misc{reference.wolfram_2025_regionwithin, author="Wolfram Research", title="{RegionWithin}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RegionWithin.html}", note=[Accessed: 26-March-2025 ]}

✖
@misc{reference.wolfram_2025_regionwithin, author="Wolfram Research", title="{RegionWithin}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RegionWithin.html}", note=[Accessed: 26-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_regionwithin, organization={Wolfram Research}, title={RegionWithin}, year={2017}, url={https://reference.wolfram.com/language/ref/RegionWithin.html}, note=[Accessed: 26-March-2025 ]}

✖
@online{reference.wolfram_2025_regionwithin, organization={Wolfram Research}, title={RegionWithin}, year={2017}, url={https://reference.wolfram.com/language/ref/RegionWithin.html}, note=[Accessed: 26-March-2025 ]}