RegionDisjoint[reg1,reg2]
returns True if the regions reg1 and reg2 are disjoint.
RegionDisjoint[reg1,reg2,reg3,…]
returns True if the regions reg1, reg2, reg3, … are pairwise disjoint.


RegionDisjoint
RegionDisjoint[reg1,reg2]
returns True if the regions reg1 and reg2 are disjoint.
RegionDisjoint[reg1,reg2,reg3,…]
returns True if the regions reg1, reg2, reg3, … are pairwise disjoint.
Details and Options

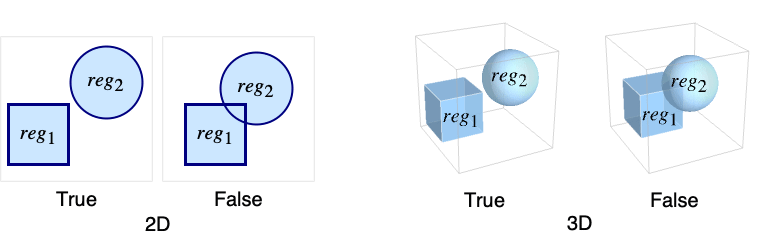
- The regions reg1 and reg2 are disjoint if there are no points that belong to both reg1 and reg2.
- If all regi are parameter-free regions, i.e. ConstantRegionQ[regi] is True, the regions are point sets, and typically True or False is returned.
- If some regi depend on parameters, i.e. ConstantRegionQ[regi] is False, then regi represents a family of regions, and RegionDisjoint will attempt to compute conditions on parameters such that the regions are disjoint.
- The following options can be given:
-
Assumptions $Assumptions assumptions to make about parameters GenerateConditions False whether to generate conditions on parameters
Examples
open all close allBasic Examples (2)
Scope (17)
Basic Uses (5)
Basic Regions (4)
Regions in ![]() including Line and Interval:
including Line and Interval:
Ball:
Regions in ![]() including Point:
including Point:
Line:
Rectangle and RegularPolygon:
Regions in ![]() including Point:
including Point:
Line:
Cuboid and Hexahedron:
Tetrahedron and Simplex:
Regions in ![]() including Cuboid and Parallelepiped in
including Cuboid and Parallelepiped in ![]() :
:
Formula Regions (4)
Mesh Regions (3)
Compare MeshRegion in ![]() :
:
Compare BoundaryMeshRegion in ![]() :
:
Compare MeshRegion with BoundaryMeshRegion in ![]() :
:
Derived Regions (1)
Compare BooleanRegion:
Options (2)
Applications (6)
Estimate ![]() by simulating Buffon's needle problem:
by simulating Buffon's needle problem:
Create randomly orientated line segments of length ![]() :
:
Select line segments that overlap the grid of lines:
Visualize overlapping line segments (red):
Detect collisions between an object and a collection of walls:
Color walls that do not collide with the cow green, and red otherwise:
Find all countries that share a border with France:
Select the countries whose polygons are not disjoint from France's polygon:
View these countries on a map:
Find and visualize all positions where a unit rectangle is disjoint from an annulus:
Perform a random walk outside of a region:
Define a function to walk a point in a random direction, staying outside of a region:
Simulate a random walk from an initial point:
Create a network that connects two US states if they share a border:
Two state's polygons share a border when RegionDisjoint returns False:
Style this network atop a map of the United States:
The largest disconnect is between Maine and the westernmost states:
Properties & Relations (4)
A region and its complement are always disjoint:
Disjoint regions share no common point:
For non‐empty regions, RegionEqual and RegionWithin return False when RegionDisjoint returns True:
Use FindInstance to find points that lie in the intersection of two regions:
Use RandomPoint to find a uniform sampling of points that lie in the intersection of two regions:
Use Reduce to find where two regions overlap:
Related Guides
History
Text
Wolfram Research (2017), RegionDisjoint, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionDisjoint.html.
CMS
Wolfram Language. 2017. "RegionDisjoint." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionDisjoint.html.
APA
Wolfram Language. (2017). RegionDisjoint. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionDisjoint.html
BibTeX
@misc{reference.wolfram_2025_regiondisjoint, author="Wolfram Research", title="{RegionDisjoint}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RegionDisjoint.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_regiondisjoint, organization={Wolfram Research}, title={RegionDisjoint}, year={2017}, url={https://reference.wolfram.com/language/ref/RegionDisjoint.html}, note=[Accessed: 25-January-2026]}