Simplex

Simplex[{p1,…,pk}]

represents the simplex spanned by points pi.

Details and Options

  • Simplex is also known as point, line segment, triangle, tetrahedron, pentachoron, hexateron, etc.
  • Simplex represents all convex combinations of the given points 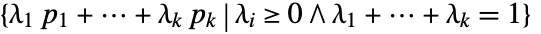. The region is 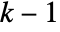dimensional when 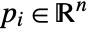are affinely independent and .
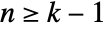  • Example simplices where rows correspond to embedding dimension:
  • Simplex[n] for integer n is equivalent to Simplex[{{0,…,0},{1,0,…,0},…,{0,…,0,1}}], the unit standard simplex in .
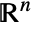  • Simplex can be used as a geometric region and graphics primitive.
  • In graphics, the points pi can be Scaled and Dynamic expressions.
  • Graphics rendering is affected by directives such as FaceForm, EdgeForm, Opacity, and color.

Examples

open allclose all

Basic Examples  (3)

A Simplex in 3D:

And in 2D:

Different styles applied to a simplex:

Volume and centroid:

Scope  (20)

Graphics  (9)

Specification  (3)

A standard unit Simplex in 3D:

A 2D simplex spanning three points:

A simplex in dimensions is specified by at most points:

Styling  (3)

Different styles applied to a simplex:

Color directives specify the face color:

FaceForm and EdgeForm can be used to specify the styles of the faces and edges:

Coordinates  (3)

Specify coordinates by fractions of the plot range:

Specify scaled offsets from the ordinary coordinates:

Points can be Dynamic:

Regions  (11)

Embedding dimension is the dimension of the space in which the simplex lives:

Geometric dimension is the dimension of the shape itself:

Point membership test:

Get conditions for point membership:

Measure and centroid:

The measure for a standard simplex in dimension is :

Distance from a point:

Visualize it:

Signed distance from a point:

Nearest point to the region:

Visualize it:

A simplex is bounded:

Find its range:

Integrate over a simplex:

Optimize over a simplex:

Solve equations constrained by a simplex:

Applications  (1)

Define the Kuhn simplex for dimension :

The 2D Kuhn simplex:

The 3D Kuhn simplex:

The measure in dimension is :

The centroid in dimension is :

Properties & Relations  (8)

TriangulateMesh can be used to decompose a volume mesh into simplices:

Use options such as MaxCellMeasure to control the number of simplices:

Point is a special case of Simplex:

Line is a special case of Simplex:

Triangle is a special case of Simplex:

Tetrahedron is a special case of Simplex:

Polygon is a generalization of Simplex in dimension 2:

ImplicitRegion can represent any Simplex:

Simplex is the set of convex combinations of its vertices:

Neat Examples  (1)

Random collection of simplices:

Wolfram Research (2014), Simplex, Wolfram Language function, https://reference.wolfram.com/language/ref/Simplex.html.

Text

Wolfram Research (2014), Simplex, Wolfram Language function, https://reference.wolfram.com/language/ref/Simplex.html.

CMS

Wolfram Language. 2014. "Simplex." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Simplex.html.

APA

Wolfram Language. (2014). Simplex. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Simplex.html

BibTeX

@misc{reference.wolfram_2025_simplex, author="Wolfram Research", title="{Simplex}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Simplex.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_simplex, organization={Wolfram Research}, title={Simplex}, year={2014}, url={https://reference.wolfram.com/language/ref/Simplex.html}, note=[Accessed: 21-February-2025 ]}