TriangulateMesh

TriangulateMesh[mr]

generates a triangulation of the mesh region mr.

Details and Options

  • TriangulateMesh is also known as triangulation, tetrahedralization, simplicial decomposition, mesh generation and mesh refinement.
  • Typically used to generate a partition of a region into lines (1D), triangles (2D) or tetrahedra (3D) optimized to some criteria.
  • TriangulateMesh has the same options as MeshRegion, with the following additions and changes:
  • MaxCellMeasure Automaticmaximum cell measure
    MeshQualityGoal Automaticquality goal for mesh cells
    MeshRefinementFunction Nonefunction that returns True if a mesh cell needs refinement
    MethodAutomaticmethod to use
    PerformanceGoal$PerformanceGoalwhether to consider speed or quality
  • Possible settings for the Method option include:
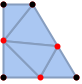
  • "ConformingDelaunay"triangulation that satisfies the Delaunay condition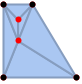
    "ConstrainedDelaunay"triangulation that preserves original 1D boundary cells and almost satisfies the Delaunay condition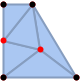
    "ConstrainedQuality"triangulation that adds fewer 0D cells and almost satisfies the Delaunay condition
  • A triangulation 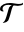of a mesh mr satisfies the Delaunay condition if no original point on the boundary of mr is inside the circumsphere of any simplex in .

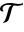Examples

open allclose all

Basic Examples  (3)

Triangulate a BoundaryMeshRegion in 1D:

Control the cell quality and sizes by using options:

Triangulate a BoundaryMeshRegion in 2D:

Control the cell quality and sizes by using options:

Triangulate a BoundaryMeshRegion in 3D:

Control the cell quality and sizes by using options:

Scope  (4)

Triangulate a BoundaryMeshRegion in 1D:

In 2D:

In 3D:

Triangulate a MeshRegion in 1D:

In 2D:

In 3D:

TriangulateMesh works individually on dimensional components:

MaxCellMeasure controls the maximum size a cell in the triangulation can be:

The measure used is arc length for 1D meshes, area for 2D, and volume for 3D:

Options  (28)

MaxCellMeasure  (6)

Set different length constraints for a 1D region:

Set different area constraints for a 2D region:

The areas for the different triangles:

Set an edge length constraint for a 2D region:

The lengths for different edges:

Set a volume constraint for a 3D region:

The volumes for different tetrahedra:

Set a face area constraint for a 3D region:

The areas for different faces:

Set an edge length constraint for a 3D region:

The lengths for different edges:

MeshCellHighlight  (3)

MeshCellHighlight allows you to specify highlighting for parts of a TriangulateMesh:

By making faces transparent, the internal structure of a 3D MeshRegion can be seen:

Individual cells can be highlighted using their cell index:

Or by the cell itself:

MeshCellLabel  (3)

MeshCellLabel can be used to label parts of a TriangulateMesh:

Label the vertices and edges of a polygon:

Individual cells can be labeled using their cell index:

Or by the cell itself:

MeshCellMarker  (1)

MeshCellMarker can be used to assign values to parts of a TriangulateMesh:

Use MeshCellLabel to show the markers:

MeshCellShapeFunction  (2)

MeshCellShapeFunction allows you to specify functions for parts of a TriangulateMesh:

Individual cells can be drawn using their cell index:

Or by the cell itself:

MeshCellStyle  (3)

MeshCellStyle allows you to specify styling for parts of a TriangulateMesh:

By making faces transparent, the internal structure of a 3D MeshRegion can be seen:

Individual cells can be highlighted using their cell index:

Or by the cell itself:

MeshQualityGoal  (4)

The default setting is Automatic:

Generate a "Minimal" quality triangulation:

Generate a "Maximal" quality triangulation:

Explicitly set a quantitative quality goal:

MeshRefinementFunction  (4)

Use MeshRefinementFunction to make the edges smaller left of the origin:

Use MeshRefinementFunction to make the triangles in the first quadrant smaller:

Set a continuously varying area constraint:

Discretize the region more finely in the first orthant:

PlotTheme  (2)

Use a theme with grid lines and a legend:

Use a theme to draw a wireframe:

Applications  (4)

Triangulate a polygon:

A minimal triangulation:

Triangulate the basic 3D primitives:

Minimal triangulations:

Triangulate inside the boundary of Monaco:

Triangulate using a minimal number of triangles:

Triangulate so that the maximum area is at most :

A nonlinear transformation of a region can be approximated by transforming vertices:

Because there are few vertices in the mesh, the transformation is poorly approximated:

By triangulating, a more accurate approximation may be made:

Properties & Relations  (2)

The output of TriangulateMesh is always a MeshRegion:

The cells in the output of TriangulateMesh are always simplices:

In 2D, simplices are triangles:

Wolfram Research (2014), TriangulateMesh, Wolfram Language function, https://reference.wolfram.com/language/ref/TriangulateMesh.html (updated 2020).

Text

Wolfram Research (2014), TriangulateMesh, Wolfram Language function, https://reference.wolfram.com/language/ref/TriangulateMesh.html (updated 2020).

CMS

Wolfram Language. 2014. "TriangulateMesh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/TriangulateMesh.html.

APA

Wolfram Language. (2014). TriangulateMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TriangulateMesh.html

BibTeX

@misc{reference.wolfram_2024_triangulatemesh, author="Wolfram Research", title="{TriangulateMesh}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/TriangulateMesh.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_triangulatemesh, organization={Wolfram Research}, title={TriangulateMesh}, year={2020}, url={https://reference.wolfram.com/language/ref/TriangulateMesh.html}, note=[Accessed: 21-December-2024 ]}