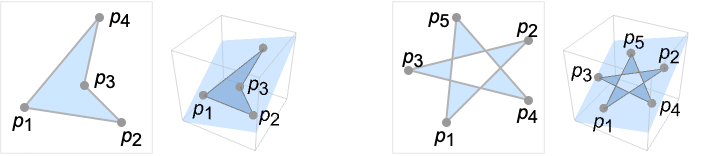
Polygon[{p1,…,pn}]
represents a filled polygon with points pi.
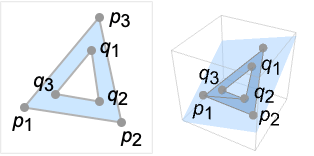
Polygon[{p1,…,pn}{{q1,…,qm},…}]
represents a polygon with holes {q1,…,qm},….
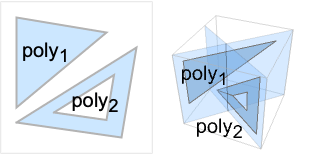
Polygon[{poly1,poly2,…}]
represents a collection of polygons polyi.
Polygon[{p1,…,pn},data]
represents a polygon in which coordinates given as integers i in data are taken to be pi.


Polygon
Polygon[{p1,…,pn}]
represents a filled polygon with points pi.
Polygon[{p1,…,pn}{{q1,…,qm},…}]
represents a polygon with holes {q1,…,qm},….
Polygon[{poly1,poly2,…}]
represents a collection of polygons polyi.
Polygon[{p1,…,pn},data]
represents a polygon in which coordinates given as integers i in data are taken to be pi.
Details and Options



- Polygon can be used as a geometric region and a graphics primitive.
- Polygon[{p1,…,pn}] is a plane region, representing all the points inside the closed curve with line segments {p1,p2},…,{pn-1,pn} and {pn,p1}.
- A point is an element of the polygon if a ray from the point in any direction in the plane crosses the boundary line segments an odd number of times.
- Polygon[{p1,…,pn}{{q1,…,qm},…}] specifies a polygon with holes consisting of an outer polygon Polygon[{p1,…,pn}] and one or several inner polygons Polygon[{q1,…,qm}],….
- A point is an element of the polygon if it is in the outer polygon but not in any inner polygon.
- Polygon[{poly1,poly2,…}] is a collection of polygons polyi with or without holes and is treated as a union of polyi for geometric computations.
- Polygon[{p1,…,pn},data] effectively replaces integers i that appear as coordinates in data by the corresponding pi.
-
Polygon[{p1,…,pn},{b1,…,bn}] polygon boundary points {pb1,…,pbk} Polygon[{p1,…,pn},{{o1,…,ok}{{i1,…,il},…}] outer polygon boundary points {po1,…,pok} and inner polygon boundary {pi1,…,pil} etc. Polygon[{p1,…,pn},{{b1,…,bn},{o1,…,ok}{{i1,…,il},…},…}] a collection of several polygons - As a geometric region, the points pi can have any embedding dimension, but must all lie in a plane and have the same embedding dimension.
- In a graphic, the points pi can be Scaled, Offset, ImageScaled and Dynamic expressions.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, Texture, Specularity, Opacity and color.
- FaceForm[front,back] can be used to specify different styles for the front and back of polygons in 3D. The front is defined by the right-hand rule and the direction of the first three points.
- The following options and settings can be used in graphics:
-
VertexColors Automatic vertex colors to be interpolated VertexNormals Automatic effective vertex normals for shading VertexTextureCoordinates None coordinates for textures - Polygon can be used with symbolic points in GeometricScene.
Examples
open all close allScope (21)
Graphics (11)
Styling (6)
Color directives specify the face colors of polygons:
Texture can be used to specify a texture to be used on the faces of polygons:
Texture can work together with different Opacity:
Texture can work together with different Lighting:
FaceForm and EdgeForm can be used to specify the styles of the interiors and boundaries:
In 3D, different properties can be specified for the front and back of faces using FaceForm:
Use FaceForm to set front and back textures differently in 3D:
Colors can be specified at vertices using VertexColors:
Normals can be specified at vertices using VertexNormals for 3D polygons:
Coordinates (3)
Regions (10)
Get conditions for point membership:
Integrate over a polygon:
Options (7)
VertexNormals (1)
VertexTextureCoordinates (4)
Texture mapping with 2D polygons:
Texture mapping with 3D polygons:
Repeat a texture by using non-unified texture coordinate values:
Texture mapping is preceded by VertexColors:
Applications (3)
Define a polygon with ![]() vertices:
vertices:
Get face polygons from PolyhedronData:
Properties & Relations (4)
Possible Issues (3)
See Also
PolygonCoordinates OuterPolygon InnerPolygon Triangle Rectangle Parallelogram RegularPolygon Simplex CrossingPolygon WindingPolygon CanonicalizePolygon RandomPolygon MeshRegion GeometricScene
Function Repository: Trapezoid Rhombus SphericalPolygon HyperbolicPoincarePolygon NotchedPolygon RoundedPolygon PrimitiveToPolygons PerforatePolygons PolygonNormalVector
History
Introduced in 1988 (1.0) | Updated in 1996 (3.0) ▪ 2019 (12.0)
Text
Wolfram Research (1988), Polygon, Wolfram Language function, https://reference.wolfram.com/language/ref/Polygon.html (updated 2019).
CMS
Wolfram Language. 1988. "Polygon." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Polygon.html.
APA
Wolfram Language. (1988). Polygon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Polygon.html
BibTeX
@misc{reference.wolfram_2025_polygon, author="Wolfram Research", title="{Polygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Polygon.html}", note=[Accessed: 19-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_polygon, organization={Wolfram Research}, title={Polygon}, year={2019}, url={https://reference.wolfram.com/language/ref/Polygon.html}, note=[Accessed: 19-February-2026]}