-
See Also
- SolidData
- SpherePoints
- Graphics3D
- RegionPlot3D
- Polygon
- Polyhedron
- GraphData
-
- Entity Types
- Polyhedron
-
- Interpreter Types
- Polyhedron
- PolyhedronClass
- ComputedPolyhedron
- Related Guides
PolyhedronData[poly,"property"]
gives the value of the specified property for the polyhedron named poly.
PolyhedronData[poly]
gives an image of the polyhedron named poly.
PolyhedronData["class"]
gives a list of the polyhedra in the specified class.


PolyhedronData
PolyhedronData[poly,"property"]
gives the value of the specified property for the polyhedron named poly.
PolyhedronData[poly]
gives an image of the polyhedron named poly.
PolyhedronData["class"]
gives a list of the polyhedra in the specified class.
Details










- Polyhedra can be specified by standard names such as "Dodecahedron" and "TruncatedCube".
- Classes of polyhedra supported include "Platonic", "Archimedean", "ArchimedeanDual", "KeplerPoinsot", "Johnson", and "Uniform".
- PolyhedronData includes polyhedron compounds.
- PolyhedronData[] and PolyhedronData[All] give a list of all available polyhedra.
- PolyhedronData[patt] gives a list of all polyhedron standard names that match the string pattern patt.
- PolyhedronData[n] gives a list of polyhedra with n faces, with faces not necessarily being convex.
- PolyhedronData[;;n] gives a list of polyhedra with ≤n faces.
- PolyhedronData[m;;n] gives a list of all standard polyhedra with m through n faces.
- PolyhedronData["class",n], etc. gives a list of polyhedra in the specified class with n faces, etc.
- PolyhedronData["Classes"] gives a list of all supported classes.
- PolyhedronData["Properties"] gives a list of properties available for polyhedra.
- For coordinate purposes, all polyhedra are taken to have smallest edges of unit length.
- Overall properties include:
-
"Classes" classes of which the polyhedron is a member "NotationRules" index notations for the polyhedron - Structural properties include:
-
"VertexCoordinates" list of vertex coordinates "EdgeIndices" list of edges (as vertex index pairs) "FaceIndices" list of faces (as vertex index lists) - Geometric primitives properties include:
-
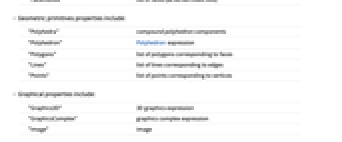
"Polyhedra" compound polyhedron components "Polyhedron" Polyhedron expression "Polygons" list of polygons corresponding to faces "Lines" list of lines corresponding to edges "Points" list of points corresponding to vertices - Graphical properties include:
-
"Graphics3D" 3D graphics expression "GraphicsComplex" graphics complex expression "Image" image - Combinatorial properties include:
-
"EdgeCount" total number of edges "FaceCount" total number of faces "VertexCount" total number of vertices "NetCount" number of topologically distinct nets that can be drawn - Region-related properties include:
-
"BoundaryMeshRegion" boundary mesh representation "CoordinateBounds" coordinate bounds "ImplicitRegion" representation as inequalities and equalities "MeshRegion" mesh representation "Region" geometric region "RegionFunction" pure function giving True in the interior of the polyhedron - Geometrical properties include:
-
"Centroid" coordinates of the centroid in the standard embedding "Circumcenter" center of circumscribed sphere "Circumdiameter" twice the circumradius "Circumradius" circumradius assuming unit smallest edge length "Circumsphere" graphics primitive for the circumscribed sphere "DehnInvariant" Dehn invariant "DihedralAngles" dihedral angles "GeneralizedDiameter" maximum distance between a pair of vertices "Incenter" center of inscribed sphere "InertiaTensor" inertia tensor of the solid polyhedron assuming unit mass "Inradius" inradius assuming unit smallest edge length "Insphere" inscribed sphere "Midcenter" center of reciprocating sphere "Midradius" midradius assuming unit smallest edge length "Midsphere" graphics primitive for the reciprocating sphere "StableFaces" stable faces "SurfaceArea" total surface area assuming unit smallest edge length "UnstableFaces" unstable faces "VertexSubsetHulls" rules for vertices whose hulls form other solids "Volume" enclosed volume assuming unit smallest edge length - Average length properties include:
-
"MeanCylindricalRadius" average of 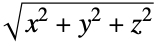 over the polyhedral region
over the polyhedral region"MeanInteriorLineSegmentLength" average length of a line segment whose endpoints are picked at random in the polyhedral region "MeanSphericalRadius" average of 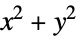 over the polyhedral region
over the polyhedral region"MeanSquareCylindricalRadius" average of 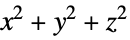 over the polyhedral region
over the polyhedral region"MeanSquareSphericalRadius" average of 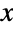 over the polyhedral region
over the polyhedral region - PolyhedronData[name,"class"] gives True if the polyhedron is in the specified class.
- Classes of polyhedra include:
-
"Amphichiral" amphichiral solid "Canonical" polyhedron with a midsphere "Chiral" chiral solid "Compound" compound of two or more polyhedra "Concave" concave solid "Convex" convex solid "Deltahedron" solid consisting of congruent equilateral triangles "Equilateral" all sides have unit length "Isohedron" symmetries act transitively on polyhedron faces "Parallelohedron" parallelohedron "Plesiohedron" plesiohedron "SelfDual" polyhedron is its own dual "Simple" simple polyhedron "SpaceFilling" space-filling polyhedron "Stellation" stellation of a polyhedron "Stereohedron" stereohedron "Toroidal" toroidal polyhedron "Unistable" unistable polyhedron "Zonohedron" zonohedron - Classes of polyhedra that are members of finite families include:
-
"Archimedean" one of the 13 Archimedean solids "ArchimedeanDual" one of the 13 Archimedean duals "Johnson" one of the 92 Johnson solids "KeplerPoinsot" one of the 4 Kepler-Poinsot solids "Platonic" one of the 5 Platonic solids "PlatonicDual" one of the 5 Platonic duals "Trapezohedron" canonical trapezohedron "Uniform" one of the 80 uniform polyhedra "UniformDual" one of the 80 uniform duals "Zalgaller" one of the 28 Zalgaller polyhedra - Classes of polyhedra indexed by an integer include:
-
"Antiprism" antiprism "Dipyramid" dipyramid "Prism" prism "Pyramid" pyramid - Naming-related properties include:
-
"AlternateNames" alternate English names, as strings "AlternateStandardNames" alternate standard Wolfram Language names "Name" English name as a string "Names" English name and alternate names "Entity" polyhedron entity "StandardName" standard Wolfram Language name - PolyhedronData[name,"property","outputtype"] gives polyhedron properties in the format specified by "outputtype", which, depending on "property", may be "Adjacent", "Coordinates", "Count", "Entity", "Graph", "Graphics3D", "GraphicsComplex", "Group", "Image", "Length", "Line", "List", "Name", "Notation", "Point", "Polygon", "Polyhedron", "Rule", "Tally", or "Undirected".
- Output types related to polyhedron output and display include:
-
"CompoundInterior" interior (common volume) of a polyhedron compound as a graphic, graphics complex, polyhedron or scale "ConvexHull" convex hull as a graphic, graphics complex, polyhedron or scale "DihedralAngles" dihedral angles as a list of angles or set of rules indexed by adjacent face indices "Dual" polyhedron dual as an entity standard name, entity, graphic, graphics complex, polyhedron, or scale "Edges" edges as an indexed list, count, list of unique lengths, rule list, lines, graphic, graphics complex, or image "Faces" faces as an indexed list, count, list of adjacent face indices, rule list of edge count tallies, polygons, graphic, graphics complex, or image "Hull" (not necessarily convex) hull as a graphic, graphics complex, polyhedron, or scale "Net" polyhedron net as a graphic, graphics compex, image, list of vertex coordinates, count, list of face indices, or graph "Skeleton" skeleton graph as a graph, vertex coordinate list, image, graph entity standard name, graph entity, edge rule list, or undirected edge list "SymmetryGroup" symmetry group as a group standard name, or entity "Vertices" vertices as indices, count, point, graphics, graphics complex, or image - PolyhedronData[name,"property","ann"] or PolyhedronData["property","ann"] gives various annotations associated with a property. Typical annotations include:
-
"Description" short textual description of the property "Information" hyperlink to additional information "LongDescription" longer textual description of the property "Value" the value of the property
Examples
open all close allBasic Examples (6)
Show a graphic of the regular dodecahedron:
Show the net of the regular dodecahedron:
Show the snub cube with colored faces and transparency with no external lighting:
Show the snub cube with colored faces and transparency in the presence of external lighting:
Count the number of edges of a regular icosahedron:
Do the same using the "Count" annotation:
Scope (171)
Entities (4)
Return a 3D graphic of the cube polyhedron entity:
Query for the surface area of a unit cube using EntityValue:
Do the same with full property syntax:
Compare with the PolyhedronData call:
Use PolyhedronData directly to query for members of a class:
Return the members as a set of polyhedron entities using EntityClass and EntityList:
Use an implicitly defined entity class to return entities satisfying a set of constraints:
Names and Classes (6)
Properties and Annotations (2)
Property Values (2)
Detailed Properties (87)
Structural Properties (3)
Geometric Primitives Properties (4)
Give the regular octahedron as a Polyhedron object:
Return the polygons corresponding to the faces of the cube:
Return the lines corresponding to the edges of the octahedron:
Return the points corresponding to the vertices of the cube:
Graphical Properties (4)
Combinatorial Properties (4)
Region-Related Properties (7)
Give the boundary mesh region of the small triambic icosahedron:
Return the coordinate bounds of the icosahedron:
Place a bounding box around the solid:
Use the bounds to plot the relevant region:
Give the implicit region of the cube:
Give the mesh region of the small triambic icosahedron:
Visualize the region of the small triambic icosahedron:
Give the region function of the tetrahedron:
Visualize the region by converting it to an ImplicitRegion:
Give the region function of the cuboctahedron as a pure function:
Give the region function of the cuboctahedron as a function of ![]() ,
, ![]() , and
, and ![]() coordinates:
coordinates:
Plot the region corresponding to the interior of the cuboctahedron:
Geometrical Properties (20)
Give the centroid of Dürer's solid:
Give the circumcenter of the unit tetrahedron:
Show the circumdiameter of the unit tetrahedron:
Show the circumradius of the unit tetrahedron:
Combine the two to get the circumsphere itself:
Show the circumsphere of the unit cube:
Show the Dehn invariant of the unit cube:
The Dehn invariant of a space-filling polyhedron is 0:
Show the dihedral angle rules of the unit cube:
Give the generalized diameter of the unit cube:
Give the incenter of the unit cube:
Give the normalized moment of inertia tensor of the Wolfram Language polyhedron:
Give the inradius of the unit cube:
Combine the two to get the insphere of the unit cube:
Give the midcenter of the unit cube:
Give the midradius of the unit cube:
Combine the two to get the midsphere of the unit cube:
Show the stable face of the Conway–Guy polyhedron:
Give the surface area of the unit cube:
Show the unstable faces of the Conway–Guy polyhedron:
Give rules for vertex subsets whose convex hulls form other solids:
Average Length Properties (5)
Finite Families (9)
Naming-Related Properties (7)
List the alternate English names of the cube:
List the alternate standard names for the octahedron:
Give the entity form of the cube:
Give the textual name of the cube:
Give the textual names of the cube:
Give rules for various notations for the cube:
Query the standard name of the 3-hypercube:
Show other alternate standard names corresponding to this standard name:
Annotated Properties (70)
"CompoundInterior" (1)
"ConvexHull" (1)
"DihedralAngles" (2)
"Dual" (7)
"DualCompound" (6)
"Edges" (11)
List the indices of the edges of the equilateral 5-prism:
Visualize the edge connectivity as a graph embedded in three dimensions:
Return the number of edges as an annotation:
Do the same using the dedicated property:
Return edges as a graphics expression:
Return the underlying graphics expression:
Return a sorted list of unique edge lengths:
Give edge lengths of the deltoidal hexecontahedron:
Return edges as explicit line segments:
Explicitly request edge indices as a list of pairs:
Return edges as a list of indexed rules:
Plot using GraphPlot:
Return edges as a list of undirected edges:
Convert to a Graph expression:
"Faces" (11)
List the indices of a square pyramid's faces:
Return a list of indices of adjacent faces:
Return the number of faces as an annotation:
Do the same using the dedicated property:
Return a graphics expression containing the faces:
Return the underlying graphics expression:
Explicitly request faces as a list of indices:
Return faces as explicit polygons:
Do the same using the "Polygons" property:
Return a rule list of counts of faces with given numbers of sides:
Show faces colored by numbers of sides:
"Net" (11)
Show a styled graphics expression for the icosahedron net:
Do the same using the explicit "Graphics" annotation:
Show a net colored by face type:
Give the coordinates of the vertices of an icosahedron net:
Return the number of nonisomorphic nets for the cube:
Do the same using the dedicated property:
Return the net of the dodecahedron as a Graph object:
Show a graphic for the cuboctahedron net:
Give the faces in a net of the octahedron as a GraphicsComplex:
Give the edges of an icosahedron net as a GraphicsComplex:
Give the indices of the faces of a net of the icosahedron:
Construct a graphic from the net faces:
"Polyhedron" (1)
"Skeleton" (8)
Return the skeleton graph of the dodecahedron:
Give the vertices of a skeleton of the dodecahedron:
Obtain the skeleton graph as an Entity:
Return the skeleton of the dodecahedron as a Graph object:
This is equivalent to the default output of "Skeleton":
Give the name of the skeleton graph of the cube:
Give dodecahedron skeleton graph edges as rules:
Visualize using GraphPlot:
Visualize using GraphPlot3D:
Return the skeleton graph edges as an UndirectedEdge list:
"SymmetryGroup" (4)
Show the symmetry group of the cube as a FiniteGroupData standard name:
Do the same using the explicit "Name" annotation:
"Vertices" (7)
List the indices of a unit tetrahedron's vertices:
Compare with the "VertexCoordinates" property:
Compare with the "Coordinates" annotation:
Do the same using the "Points" property:
Return the number of vertices as an annotation:
Do the same using the dedicated property:
Return a graphics expression containing the faces:
Return the underlying graphics expression:
Show an image of the vertices:
Generalizations & Extensions (1)
Applications (8)
Generate a list of polyhedra on 8 faces:
Do the same using an implicitly defined entity class:
Generate a list of space-filling polyhedra on 8 faces:
Generate a list of chiral Archimedean polyhedra:
Generate a list of polyhedra on 5 or fewer faces:
Plot a sphere of radius 5/4 clipped by a dodecahedron of unit edge length:
Plot the numbers of polyhedra with different numbers of nodes available in PolyhedronData:
Visualize families of polyhedra by plotting edge count against vertex count:
Properties & Relations (8)
Starting in Version 12, Platonic solids are available via built-in functions:
Verify that an antiprism graph is the skeleton of an antiprism polyhedron:
Recognize the skeleton graph as a graph entity:
Recognize the preceding as a graph entity:
Show the 3D embedding of the graph:
Print the surface area of the octahedron:
Compute the surface area by summing the areas of its faces:
Compute the surface area by summing the areas of the faces in its net:
Compute the surface by summing over the face areas using Area:
Compute the surface area of the polyhedron:
Compare with the value obtained by applying Area to the corresponding region boundary:
Show inequalities defining the interior of the cube:
Show the cube interior as defined by inequalities:
Display the volume of the octahedron:
Compute the volume from the defining inequalities:
Compute the volume of the octahedron from the pyramids subtended by its faces:
Verify the result agrees with the volume computed by applying Volume to the region:
Display the centroid of the cube:
Compute the centroid from the defining inequalities:
Verify the result agrees with the centroid computed by applying RegionCentroid to the region:
Plot the vertices of the truncated icosahedron:
Visualize as the convex hull of its vertices:
Show the vertices and convex hull together:
Built-in polyhedron operations work with PolyhedronData objects:
Possible Issues (6)
Using nonstandard polyhedron names will not work:
Use string patterns directly in PolyhedronData:
Or use general string matching capabilities:
Using nonstandard property names will not work:
Use general string patterns to locate standard property names:
Arithmetical operations cannot be carried out on Missing entries:
Remove the Missing entries before performing operations:
Not all properties are defined for all polyhedra:
"Region" and related properties may not be available for solids with intersecting polygons:
See Also
SolidData SpherePoints Graphics3D RegionPlot3D Polygon Polyhedron GraphData
Entity Types: Polyhedron
Interpreter Types: Polyhedron PolyhedronClass ComputedPolyhedron
Related Guides
History
Introduced in 2007 (6.0) | Updated in 2008 (7.0) ▪ 2010 (8.0) ▪ 2014 (10.0) ▪ 2015 (10.2) ▪ 2016 (10.4) ▪ 2017 (11.1) ▪ 2019 (12.0) ▪ 2020 (12.1) ▪ 2020 (12.2) ▪ 2021 (13.0) ▪ 2022 (13.1) ▪ 2024 (14.0) ▪ 2024 (14.1)
Text
Wolfram Research (2007), PolyhedronData, Wolfram Language function, https://reference.wolfram.com/language/ref/PolyhedronData.html (updated 2024).
CMS
Wolfram Language. 2007. "PolyhedronData." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/PolyhedronData.html.
APA
Wolfram Language. (2007). PolyhedronData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PolyhedronData.html
BibTeX
@misc{reference.wolfram_2025_polyhedrondata, author="Wolfram Research", title="{PolyhedronData}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/PolyhedronData.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_polyhedrondata, organization={Wolfram Research}, title={PolyhedronData}, year={2024}, url={https://reference.wolfram.com/language/ref/PolyhedronData.html}, note=[Accessed: 03-March-2026]}