WindingPolygon

WindingPolygon[{p1,p2,…,pn}]

gives a polygon representing all points for which the closed contour p1,p2,…,pn,p1 winds around at least once.

WindingPolygon[{{p11,p12,…},{p21,p22,…},…}]

gives a polygon from the closed contours p11,p12,… and p21,p22,….

WindingPolygon[…,"wrule"]

uses the specified winding rule "wrule" to define the polygon.

Details and Options

  • WindingPolygon is also known as winding filling rule.
  • WindingPolygon is commonly used to define a polygon from self-intersecting closed curves.
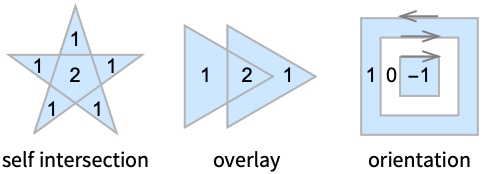
  • A point p is in the polygon if the number of revolutions of the closed contour around p is not zero. The number of revolutions is given by WindingCount.
  • The number of winding counts are given below for each region:
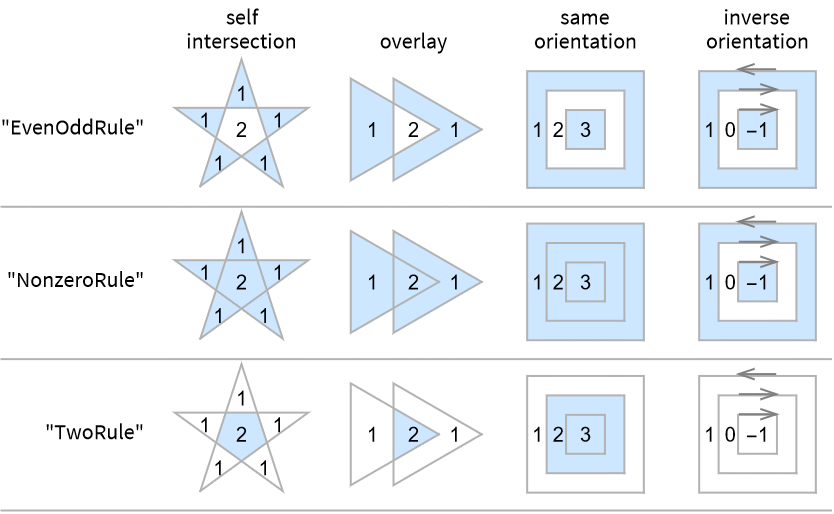
  • Different winding rules "wrule" give different polygons. Possible winding rules include:
  • WindingPolygon[{p1,p2,…}] is equivalent to WindingPolygon[{p1,p2,…},"NonzeroRule"].
  • The points pi can have any embedding dimension, but must all lie in a plane and have the same embedding dimension.
  • WindingPolygon takes the same options as Polygon.

    • List of all options

Examples

open allclose all

Basic Examples  (2)

Define a polygon:

Construct a polygon from a self-intersecting contour:

Its area:

Scope  (14)

Basic Uses  (5)

Define a two-dimensional polygon:

Three-dimensional polygons:

n-dimensional polygons:

Construct polygons from self-intersecting contours:

Multiple contours:

Nonzero Rule  (3)

Polygons:

Three-dimensional polygons:

n-dimensional polygons:

EvenOdd Rule  (3)

Polygons:

Three-dimensional polygons:

n-dimensional polygons:

Two Rule  (3)

Polygons:

Three-dimensional polygons:

n-dimensional polygons:

Options  (6)

VertexColors  (2)

Polygon with vertex colors:

Specify vertex colors for 3D polygons:

VertexNormals  (1)

Compute normal vectors using the cross-product of edge vectors:

A triangle with normals pointing in the direction {1,-1,1}:

Using different normals will affect shading:

VertexTextureCoordinates  (3)

Texture mapping with 2D polygons:

Texture mapping with 3D polygons:

Repeat a texture by using non-unified texture coordinate values:

Texture mapping is preceded by VertexColors:

Applications  (3)

Basic Applications  (1)

Geometry  (1)

Generation of regular star polygons:

Computational Geometry  (1)

Generate random polygons:

Properties & Relations  (2)

WindingPolygon is in general different than Polygon:

CrossingPolygon is an alternate polygon constructor:

Possible Issues  (2)

WindingPolygon always gives full-dimensional components:

The points in WindingPolygon must lie on a plane:

Wolfram Research (2019), WindingPolygon, Wolfram Language function, https://reference.wolfram.com/language/ref/WindingPolygon.html.

Text

Wolfram Research (2019), WindingPolygon, Wolfram Language function, https://reference.wolfram.com/language/ref/WindingPolygon.html.

CMS

Wolfram Language. 2019. "WindingPolygon." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WindingPolygon.html.

APA

Wolfram Language. (2019). WindingPolygon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WindingPolygon.html

BibTeX

@misc{reference.wolfram_2025_windingpolygon, author="Wolfram Research", title="{WindingPolygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/WindingPolygon.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_windingpolygon, organization={Wolfram Research}, title={WindingPolygon}, year={2019}, url={https://reference.wolfram.com/language/ref/WindingPolygon.html}, note=[Accessed: 21-February-2025 ]}