Ellipsoid

Ellipsoid[p,{r1,…}]

represents an axis-aligned ellipsoid centered at the point p and with semiaxes lengths ri.

Ellipsoid[p,Σ]

represents an ellipsoid centered at p and weight matrix Σ.

Details and Options

  • Ellipsoid is also known as center interval, ellipse, and hyperellipsoid.
  • Ellipsoid can be used as a geometric region and a graphics primitive.
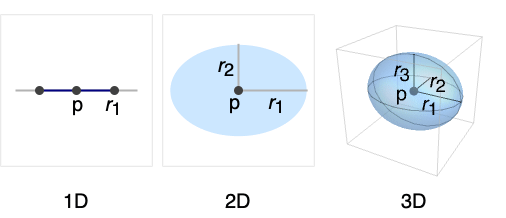
  • Ellipsoid represents the axis-aligned filled ellipsoid 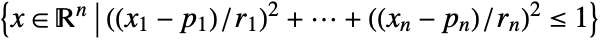or general ellipsoid .
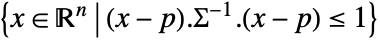  • Ellipsoid allows p to be any point in 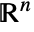, ri any positive real numbers, and Σ any real symmetric positive definite matrix.
  • Ellipsoid can be used in Graphics and Graphics3D.
  • In graphics, the points p, pi, and radii ri can be Scaled and Dynamic expressions.
  • Graphics rendering is affected by directives such as FaceForm, Specularity, Opacity, and color.

Examples

open allclose all

Basic Examples  (2)

An axis-aligned ellipsoid in 3D:

In 2D:

Measure and centroid:

Scope  (20)

Graphics  (10)

Specification  (4)

An axis-aligned ellipsoid in 3D:

In 2D:

A general ellipsoid in 3D:

In 2D:

Styling  (4)

Balls with different specular exponents:

Black ball that glows red:

Opacity specifies the face opacity:

2D styling:

Coordinates  (2)

Specify coordinates by fractions of the plot range:

Specify scaled offsets from the ordinary coordinates:

Regions  (10)

Embedding dimension is the dimension of the space in which the ball lives:

Geometric dimension is the dimension of the shape itself:

Membership testing:

Get conditions for point membership:

Volume:

Centroid:

Distance from a point:

The distance to the nearest point for an ellipse:

Signed distance from a point:

Signed distance to an ellipse:

Nearest point in the region:

Nearest points to an enclosing sphere:

An ellipsoid is bounded:

Find its range:

Integrate over an ellipsoid region:

Optimize over an ellipsoid region:

Solve equations in an ellipsoid region:

Applications  (4)

A spheroid is an ellipsoid with two equal axes:

Compute its volume:

Total mass for an ellipsoid region with density given by :

Find the mass of methanol in an Ellipsoid:

Density of methanol:

Volume of ellipsoid:

Mass of methanol in the ellipsoid:

Find a bounding Ellipsoid to a region's bounding box:

Compute the bounding box:

Compute a bounding ellipsoid to the bounding box:

Compute the difference in Volume of the bounding solids:

Visualize bounding surfaces:

Properties & Relations  (4)

Disk is a special case of Ellipsoid:

Ball is a special case of Ellipsoid:

Ellipsoid is a generalization of Ball:

ImplicitRegion can represent any Ellipsoid:

Neat Examples  (2)

Random ellipsoid collections:

Sweep an ellipsoid around an axis:

Wolfram Research (2014), Ellipsoid, Wolfram Language function, https://reference.wolfram.com/language/ref/Ellipsoid.html.

Text

Wolfram Research (2014), Ellipsoid, Wolfram Language function, https://reference.wolfram.com/language/ref/Ellipsoid.html.

CMS

Wolfram Language. 2014. "Ellipsoid." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Ellipsoid.html.

APA

Wolfram Language. (2014). Ellipsoid. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Ellipsoid.html

BibTeX

@misc{reference.wolfram_2024_ellipsoid, author="Wolfram Research", title="{Ellipsoid}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Ellipsoid.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ellipsoid, organization={Wolfram Research}, title={Ellipsoid}, year={2014}, url={https://reference.wolfram.com/language/ref/Ellipsoid.html}, note=[Accessed: 21-November-2024 ]}