BoundingRegion

BoundingRegion[{pt1,pt2,…}]

gives the minimal axis-aligned bounding box for the points pt1, pt2, ….

BoundingRegion[{pt1,pt2,…},form]

gives a bounding region of type form.

BoundingRegion[reg,form]

gives a bounding region for the region reg.

Details and Options

  • BoundingRegion is also known as enclosing region or circumscribed region.
  • A bounding region 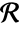for a set of points 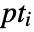is a region such that .
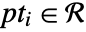  • Optimal bounding regions typically minimize some property for the bounding region, such as the minimum area oriented rectangle. They generally take longer to compute.
  • Fast bounding regions typically provide a bounding region quickly for a large number of points but may not provide the optimal bounding region, such as the minimum area oriented rectangle.
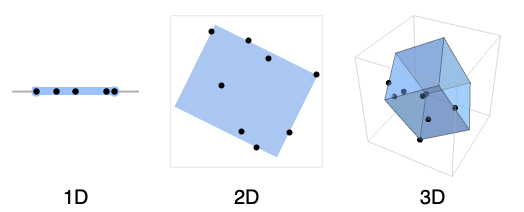
  • Possible form specifications in 1D:
  • "MinInterval"min length interval
  • Possible form specifications in 2D:
  • "MinRectangle"min area axis-aligned rectangle
    "MinOrientedRectangle"min area oriented rectangle
    "MinConvexPolygon"min area convex polygon
    "MinDisk"min area disk
    "MinEllipse"min area ellipse
    "FastOrientedRectangle"fast bounding oriented rectangle
    "FastDisk"fast bounding disk
    "FastEllipse"fast bounding ellipse
    "FastStadium"fast bounding stadium
  • Possible form specifications in 3D:
  • "MinCuboid"min volume axis-aligned cuboid
    "MinOrientedCuboid"min volume oriented cuboid
    "MinConvexPolyhedron"min volume convex polyhedron
    "MinBall"min volume ball
    "MinEllipsoid"min volume ellipsoid
    "FastOrientedCuboid"fast oriented cuboid
    "FastBall"fast ball
    "FastEllipsoid"fast ellipsoid
    "FastCylinder"fast cylinder
    "FastCapsule"fast capsule
  • Possible form specifications in nD:
  • "MinCuboid"min measure axis-aligned cuboid
    "MinBall"min measure ball
    "MinEllipsoid"min measure ellipsoid
    "FastOrientedCuboid"fast oriented cuboid
    "FastBall"fast ball
    "FastEllipsoid"fast ellipsoid
  • BoundingRegion[reg] is equivalent to BoundingRegion[reg,"MinCuboid"].
  • The following option can be given:
  • PerformanceGoal$PerformanceGoalaspects of performance to try to optimize
    WorkingPrecision MachinePrecisionprecision to use in computations

Examples

open allclose all

Basic Examples  (4)

The minimal area Disk that contains a set of points:

The minimal area Rectangle that contains a set of points:

The minimal area, arbitrarily oriented rectangle:

The minimal volume Ball that contains a set of points:

The minimal volume Cuboid that contains a set of points:

The minimal volume, arbitrarily oriented cuboid:

Scope  (28)

1D  (3)

"MinInterval" is for 1D point sets:

Works for large collections of points:

Works for mesh regions:

2D  (9)

"MinRectangle" gives the minimal area axis-aligned Rectangle:

Works for large collections of points:

"MinOrientedRectangle" gives the minimal area rectangle, not necessarily axis aligned:

Works for large collections of points:

"MinConvexPolygon" gives the minimal area polygon that contains the points:

Works for large collections of points:

"MinDisk" gives the minimal area Disk that contains the points:

Works for large collections of points:

"FastOrientedRectangle" gives an oriented bounding rectangle, which may not have the minimal area possible:

Works for large collections of points:

"FastDisk" gives a bounding Disk, which may not have the minimal area possible:

Works for large collections of points:

"FastEllipse" gives a bounding Ellipsoid, which may not have the minimal area possible:

Works for large collections of points:

"FastStadium" gives a bounding StadiumShape, not necessarily with the minimal area:

Works for large collections of points:

Find bounding regions for a mesh region:

3D  (11)

"MinCuboid" gives the minimal volume axis-aligned Cuboid:

Works for large collections of points:

"MinOrientedCuboid" gives the minimal volume cuboid, not necessarily axis aligned:

Works for large collections of points:

"MinConvexPolyhedron" gives the minimal volume polyhedron that contains the points:

Works for large collections of points:

"MinBall" gives the minimal volume Ball that contains the points:

Works for large collections of points:

"FastOrientedCuboid" gives an oriented bounding cuboid, not necessarily minimal:

Works for large collections of points:

"FastBall" gives a bounding Ball, which may not have the minimal volume possible:

Works for large collections of points:

"FastEllipsoid" gives a bounding Ellipsoid, not necessarily with the minimal volume:

Works for large collections of points:

"FastCylinder" gives a bounding Cylinder, not necessarily with the minimal volume:

Works for large collections of points:

"FastCapsule" gives a bounding CapsuleShape, not necessarily with the minimal volume:

Works for large collections of points:

Compare volumes of bounding regions:

Find bounding regions for a mesh region:

D  (5)

"MinCuboid" gives the minimal measure axis-aligned Cuboid:

Works for large collections of points:

Works for high dimensions:

"MinBall" gives the minimal measure Ball that contains the points:

Works for large collections of points:

Works for high dimensions:

Works with exact coefficients:

"FastOrientedCuboid" gives an oriented bounding cuboid, not necessarily minimal:

Works for large collections of points:

Works for high dimensions:

"FastBall" gives a bounding Ball, not necessarily with the minimal measure:

Works for large collections of points:

Works for high dimensions:

"FastEllipsoid" gives a bounding Ellipsoid, not necessarily with the minimal measure:

Works for large collections of points:

Works for high dimensions:

Options  (5)

WorkingPrecision  (5)

By default, the WorkingPrecision is MachinePrecision:

Specify lower working precision:

Specify higher working precision:

A WorkingPrecision of Infinity will evaluate a bounding region with exact calculations:

The precision of the output is limited by the precision of the input:

Use SetPrecision to increase the precision of the input, allowing for a higher-output precision:

Use Rationalize to get exact numbers. This allows for exact calculations:

Applications  (4)

Find different bounding regions for a 3D graphics object:

Compute bounding regions:

Showcase the object with its bounding regions, using the volume as label:

Find bounding regions for an arbitrary region:

Use DiscretizeRegion to discretize the region:

Compute bounding regions:

Compute random points in an arbitrary region by rejection sampling:

Find a bounding region for which random points are easy to generate:

Generate random points in the bounding region:

Select the points that belong to the original region:

Visualize the result:

Compare with points generated from the original region using RandomPoint:

Bounding regions are often used in game physics because it is simpler and faster to check for collisions between bounding regions than between the objects themselves:

Compute discretized approximations of the objects:

Show that the objects do not collide by checking that their bounding regions do not intersect:

Use FindInstance to check that the bounding regions do not intersect:

Testing for collision directly takes more time:

However, even if the objects do not collide, bounding regions may not be disjoint:

Visualize the result:

Properties & Relations  (9)

All points are members of their bounding region:

Typically, several points will be on the boundary of the bounding region:

"MinOrientedCuboid" gives smaller or equal volume than "MinCuboid":

"MinOrientedRectangle" gives smaller or equal area than "MinRectangle":

"MinConvexPolygon" will have smaller or equal area than other bounding regions:

"MinConvexPolyhedron" will have smaller or equal volume than other bounding regions:

"MinConvexPolygon" corresponds to ConvexHullMesh in 2D:

"MinConvexPolyhedron" corresponds to ConvexHullMesh in 3D:

"MinConvexPolygon" of three affinely independent points corresponds to Triangle:

"MinConvexPolyhedron" of four affinely independent points corresponds to Tetrahedron:

Circumsphere gives a circle through three points in 2D. The corresponding disk is a bounding region:

The Area for circumsphere is always greater than or equal to the area of the minimum disk:

Possible Issues  (1)

BoundingRegion may give a degenerate form of the requested region:

Wolfram Research (2016), BoundingRegion, Wolfram Language function, https://reference.wolfram.com/language/ref/BoundingRegion.html (updated 2020).

Text

Wolfram Research (2016), BoundingRegion, Wolfram Language function, https://reference.wolfram.com/language/ref/BoundingRegion.html (updated 2020).

CMS

Wolfram Language. 2016. "BoundingRegion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/BoundingRegion.html.

APA

Wolfram Language. (2016). BoundingRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BoundingRegion.html

BibTeX

@misc{reference.wolfram_2024_boundingregion, author="Wolfram Research", title="{BoundingRegion}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/BoundingRegion.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_boundingregion, organization={Wolfram Research}, title={BoundingRegion}, year={2020}, url={https://reference.wolfram.com/language/ref/BoundingRegion.html}, note=[Accessed: 30-December-2024 ]}