Circumsphere[{p1,…,pn+1}]
gives the sphere that circumscribes the points pi in ![]() .
.
Circumsphere[poly]
gives the circumsphere of a polyhedron or polygon poly.


Circumsphere
Circumsphere[{p1,…,pn+1}]
gives the sphere that circumscribes the points pi in ![]() .
.
Circumsphere[poly]
gives the circumsphere of a polyhedron or polygon poly.
Details

- Circumsphere is also known as circumcircle, circumscribed circle, or circumscribed disk.
- Circumsphere gives the Sphere of smallest measure (arc length, area, etc.) that circumscribes the points pi.
- Circumsphere evaluates to a Sphere[c,r] where the center c is known as the circumcenter, and radius r is known as the circumradius for the Simplex[{p1,…,pn+1}].
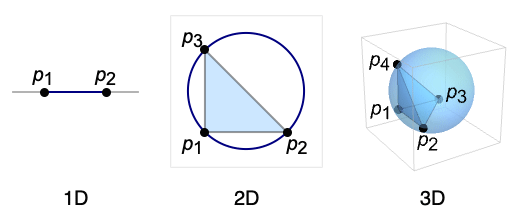
- Circumsphere is defined for
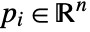 and is affinely independent.
and is affinely independent. - For polyhedra, Circumsphere[poly] is equivalent to Circumsphere[PolyhedronCoordinates[poly]].
- For polygons, Circumsphere[poly] is equivalent to Circumsphere[PolygonCoordinates[poly]].
- Circumsphere can be used with symbolic points in GeometricScene.
Examples
open all close allBasic Examples (2)
Scope (17)
Graphics (6)
Specification (2)
Circumspheres in different dimensions:
Circumsphere evaluates to a Sphere:
Regions (11)
Circumsphere works in any number of dimensions:
Get the circumcenter and circumradius:
Embedding dimension is the dimension of the space in which the sphere lives:
Geometric dimension is the dimension of the shape itself:
Get conditions for membership:
Nearest points to an enclosing sphere:
Integrate over a Circumsphere:
Solve equations over a Circumsphere:
Applications (7)
Find the intersections of a Line and a Circumsphere:
Find the intersection of two circumspheres:
Find a perpendicular bisector of a triangle:
Visualize circumcenter and bisectors in red:
The defining property of a DelaunayMesh is that no input point is contained in the circumcircle of any Triangle in the mesh:
Use Circumsphere to approximate the radius of curvature of a function:
Compare the exact radius of curvature with the radius from the circumcircle approximation:
Use a circumsphere with symbolic input to derive a formula for the radius of curvature:
The result is identical to the radius formula:
Use Circumsphere to find a disk covering for any region with a triangulation. First triangulate the region:
Use Circumsphere to compute a circle for each triangle:
Use Circumsphere to generate a ball covering for a triangulated region. First discretize and triangulate the region:
Use Circumsphere to compute spheres for each tetrahedron:
Properties & Relations (1)
Circumsphere can represent any Sphere by picking three points on a sphere in 2D:
See Also
Insphere Sphere Ball CircleThrough Triangle Polygon Tetrahedron Polyhedron Simplex ConvexHullMesh Solve GeometricScene
Function Repository: Circumcircle3D SteinerCircumellipse
Related Guides
Text
Wolfram Research (2014), Circumsphere, Wolfram Language function, https://reference.wolfram.com/language/ref/Circumsphere.html (updated 2019).
CMS
Wolfram Language. 2014. "Circumsphere." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Circumsphere.html.
APA
Wolfram Language. (2014). Circumsphere. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Circumsphere.html
BibTeX
@misc{reference.wolfram_2025_circumsphere, author="Wolfram Research", title="{Circumsphere}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Circumsphere.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_circumsphere, organization={Wolfram Research}, title={Circumsphere}, year={2019}, url={https://reference.wolfram.com/language/ref/Circumsphere.html}, note=[Accessed: 25-February-2026]}