Discriminant[poly,var]
computes the discriminant of the polynomial poly with respect to the variable var.
Discriminant[poly,var,Modulusp]
computes the discriminant modulo ![]() .
.


Discriminant
Discriminant[poly,var]
computes the discriminant of the polynomial poly with respect to the variable var.
Discriminant[poly,var,Modulusp]
computes the discriminant modulo ![]() .
.
Details and Options
- The discriminant of a polynomial with leading coefficient one is the product over all pairs of roots
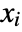 ,
, 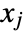 of
of 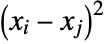 .
. - Discriminant takes the following options:
-
Method Automatic method to use Modulus 0 modulus to assume for integers - Typical possible values for Method are Automatic, "SylvesterMatrix", "BezoutMatrix", "Subresultants" and "Modular".
Examples
open all close allScope (7)
Options (4)
Applications (2)
Properties & Relations (3)
The discriminant is zero if and only if the polynomial has multiple roots:
The discriminant can be represented in terms of roots as ![]() :
:
Equation ![]() relates Discriminant and Resultant:
relates Discriminant and Resultant:
See Also
Related Guides
Text
Wolfram Research (2007), Discriminant, Wolfram Language function, https://reference.wolfram.com/language/ref/Discriminant.html (updated 2023).
CMS
Wolfram Language. 2007. "Discriminant." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/Discriminant.html.
APA
Wolfram Language. (2007). Discriminant. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Discriminant.html
BibTeX
@misc{reference.wolfram_2025_discriminant, author="Wolfram Research", title="{Discriminant}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/Discriminant.html}", note=[Accessed: 02-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_discriminant, organization={Wolfram Research}, title={Discriminant}, year={2023}, url={https://reference.wolfram.com/language/ref/Discriminant.html}, note=[Accessed: 02-March-2026]}