WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

And
✖
And

✖
e1&&e2&&…

is the logical AND function. It evaluates its arguments in order, giving False immediately if any of them are False, and True if they are all True.

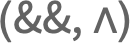
Details

  • And[e1,e2,…] can be input in StandardForm and InputForm as e1∧e2∧…. The character ∧ can be entered as &&, and, or \[And]. »
  • And has attribute HoldAll and explicitly controls the evaluation of its arguments. In e1&&e2&&…, the ei are evaluated in order, stopping if any of them are found to be False. »
  • And gives symbolic results when necessary, removing initial arguments that are True. »

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

Combine assertions with &&:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-cfai82
Out[1]=1

A symbolic conjunction:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-yi6vv
Out[1]=1

A system of equations:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-geut30
Out[1]=1

Enter using and:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-cyw7h8
Out[1]=1

Scope  (5)Survey of the scope of standard use cases

And works with any number of arguments:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-hb9gh
Out[1]=1

And is associative:

In[2]:=2
✖
https://wolfram.com/xid/0hawi-d7h0mk

And with explicit True or False arguments will simplify:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-i4iqla
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0hawi-j63r74
Out[2]=2

And evaluates its arguments in order, stopping when an argument evaluates to False:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-dmd6x9
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0hawi-dltf5i
Out[2]=2

The order of arguments may be important:

In[3]:=3
✖
https://wolfram.com/xid/0hawi-lu6s7g
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0hawi-j8qidu
Out[4]=4

Symbolic transformations will not preserve argument ordering:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-k00ay
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0hawi-c40ywc
Out[2]=2

TraditionalForm formatting:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-d2raes

Applications  (6)Sample problems that can be solved with this function

Combine conditions in Wolfram Language code:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-poaj84
In[2]:=2
✖
https://wolfram.com/xid/0hawi-jlvdi
Out[2]=2

If an argument of And evaluates to False, any subsequent arguments are not evaluated:

In[3]:=3
✖
https://wolfram.com/xid/0hawi-b6s974
Out[3]=3

The argument order in And matters; if the last two arguments are reversed, I>0 is evaluated:

In[4]:=4
✖
https://wolfram.com/xid/0hawi-m52z05
In[5]:=5
✖
https://wolfram.com/xid/0hawi-f1vek
Out[5]=5

Combine assumptions:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-8d9x7
Out[1]=1

Combine equations and inequalities; And is used both in the input and in the output:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-p9ndzd
Out[1]=1

Use And to combine conditions:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-ctbbhn
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0hawi-bbdoy
Out[2]=2

A cellular automaton based on And:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-gddzdp
Out[1]=1

Find the area of the intersection of sets given by algebraic conditions:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-fe4ca9
Out[1]=1

This shows the set:

In[2]:=2
✖
https://wolfram.com/xid/0hawi-c14dt7
Out[2]=2

Properties & Relations  (8)Properties of the function, and connections to other functions

Truth table for binary And:

In[2]:=2
✖
https://wolfram.com/xid/0hawi-ib02ro
Out[2]=2

Ternary And:

In[3]:=3
✖
https://wolfram.com/xid/0hawi-cwl4xo
Out[3]=3

Zero-argument And is True:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-9ob000
Out[1]=1

And with a single argument will return the evaluated argument regardless of value:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-g7dcos
Out[1]=1

&& has higher precedence than ||:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-lqm1sh

Use BooleanConvert to expand And with respect to Or:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-fcn3e0
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0hawi-kk4ggu
Out[2]=2

De Morgan's laws relate And, Or, and Not:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-d8jn2e
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0hawi-okqqa7
Out[2]=2

Conjunction of conditions corresponds to the product or Min of Boole functions:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-jec7qu
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0hawi-yhneo
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0hawi-bxl6ec
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0hawi-d6d5kd
Out[4]=4

Use Thread to thread over lists:

In[1]:=1
✖
https://wolfram.com/xid/0hawi-ci7k8
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0hawi-b1du8
Out[2]=2
Wolfram Research (1988), And, Wolfram Language function, https://reference.wolfram.com/language/ref/And.html (updated 1996).
✖
Wolfram Research (1988), And, Wolfram Language function, https://reference.wolfram.com/language/ref/And.html (updated 1996).

Text

Wolfram Research (1988), And, Wolfram Language function, https://reference.wolfram.com/language/ref/And.html (updated 1996).

✖
Wolfram Research (1988), And, Wolfram Language function, https://reference.wolfram.com/language/ref/And.html (updated 1996).

CMS

Wolfram Language. 1988. "And." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/And.html.

✖
Wolfram Language. 1988. "And." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/And.html.

APA

Wolfram Language. (1988). And. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/And.html

✖
Wolfram Language. (1988). And. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/And.html

BibTeX

@misc{reference.wolfram_2025_and, author="Wolfram Research", title="{And}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/And.html}", note=[Accessed: 16-April-2025 ]}

✖
@misc{reference.wolfram_2025_and, author="Wolfram Research", title="{And}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/And.html}", note=[Accessed: 16-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_and, organization={Wolfram Research}, title={And}, year={1996}, url={https://reference.wolfram.com/language/ref/And.html}, note=[Accessed: 16-April-2025 ]}

✖
@online{reference.wolfram_2025_and, organization={Wolfram Research}, title={And}, year={1996}, url={https://reference.wolfram.com/language/ref/And.html}, note=[Accessed: 16-April-2025 ]}