Not

!expr

is the logical NOT function. It gives False if expr is True, and True if it is False.

Details

  • Not[expr] can be input in StandardForm and InputForm as ¬expr. The character 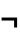¬ can be entered as !, not, or ∖[Not]. »
  • Not gives symbolic results when necessary, applying various simplification rules to them.
  • If you are using the Wolfram System with a text‐based front end, then you cannot use the notation !expr for Not[expr] if it appears at the very beginning of a line. In this case, !expr is interpreted as a shell escape. »

Examples

open allclose all

Basic Examples  (3)

Negate assertions:

Symbolic negation:

Enter using not:

Scope  (4)

Double negation simplifies to the identity:

Negate equations and inequalities:

Negate quantifiers:

TraditionalForm formatting:

Applications  (2)

Negate conditions in Wolfram Language code:

Find the area of the complement of a set given by algebraic conditions:

This shows the set:

Properties & Relations  (4)

Truth table for Not:

Use BooleanConvert to simplify the negation of Implies:

De Morgan's laws relate And, Or, and Not:

Negation of the condition for Boole function:

Possible Issues  (1)

Use parentheses to ensure ! beginning a line is not taken as a shell escape when using a terminal interface:

Wolfram Research (1988), Not, Wolfram Language function, https://reference.wolfram.com/language/ref/Not.html (updated 1996).

Text

Wolfram Research (1988), Not, Wolfram Language function, https://reference.wolfram.com/language/ref/Not.html (updated 1996).

CMS

Wolfram Language. 1988. "Not." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Not.html.

APA

Wolfram Language. (1988). Not. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Not.html

BibTeX

@misc{reference.wolfram_2025_not, author="Wolfram Research", title="{Not}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Not.html}", note=[Accessed: 25-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_not, organization={Wolfram Research}, title={Not}, year={1996}, url={https://reference.wolfram.com/language/ref/Not.html}, note=[Accessed: 25-March-2025 ]}