

Or 
Details
- Or[e1,e2,…] can be input in StandardForm and InputForm as
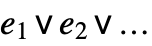 . The character
. The character 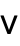 can be entered as
can be entered as  ||
|| ,
,  or
or , or \[Or].
, or \[Or]. - Or has attribute HoldAll, and explicitly controls the evaluation of its arguments. In
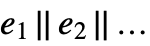 the
the 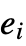 are evaluated in order, stopping if any of them are found to be True.
are evaluated in order, stopping if any of them are found to be True. - Or gives symbolic results when necessary, removing initial arguments that are False.
Examples
open all close allBasic Examples (4)
Scope (5)
Or works with any number of arguments:
Or is associative:
Or with explicit True or False arguments will simplify:
Or evaluates its arguments in order, stopping when an argument evaluates to True:
The order of arguments may be important:
Symbolic transformations will not preserve argument ordering:
TraditionalForm formatting:
Applications (6)
Combine conditions in a Wolfram Language program:
If an argument of Or evaluates to True, any subsequent arguments are not evaluated:
The argument order in Or matters; if the last two arguments are reversed, I≥0 is evaluated:
Combine equations and inequalities; Or is used both in the input and the output:
A cellular automaton based on Or:
Find the area of the union of sets given by algebraic conditions:
Properties & Relations (7)
Truth table for binary Or:
Ternary Or:
Or with a single argument will return the evaluated argument regardless of value:
&& has higher precedence than ||:
Use BooleanConvert to expand And with respect to Or:
De Morgan's laws relate And, Or, and Not:
Disjunction of conditions corresponds to the Max of Boole functions:
See Also
Xor BooleanConvert LogicalExpand BitOr Nor And Not Disjunction Union BooleanCountingFunction AnyTrue
Characters: \[Or]
Function Repository: VennDiagram
Related Guides
History
Introduced in 1988 (1.0) | Updated in 1996 (3.0)
Text
Wolfram Research (1988), Or, Wolfram Language function, https://reference.wolfram.com/language/ref/Or.html (updated 1996).
CMS
Wolfram Language. 1988. "Or." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Or.html.
APA
Wolfram Language. (1988). Or. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Or.html
BibTeX
@misc{reference.wolfram_2025_or, author="Wolfram Research", title="{Or}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Or.html}", note=[Accessed: 21-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_or, organization={Wolfram Research}, title={Or}, year={1996}, url={https://reference.wolfram.com/language/ref/Or.html}, note=[Accessed: 21-January-2026]}