RowReduce

RowReduce[m]

gives the row‐reduced form of the matrix m.

Details and Options

  • RowReduce performs a version of Gaussian elimination, adding multiples of rows together so as to produce zero elements when possible. The final matrix is in reduced row echelon form.
  • If m is a non‐degenerate square matrix, RowReduce[m] is IdentityMatrix[Length[m]]. »
  • If m is a sufficiently non‐degenerate rectangular matrix with 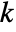rows and more than 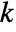columns, then the first 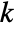columns of RowReduce[m] will form an identity matrix. »
  • RowReduce works on both numerical and symbolic matrices.
  • The following options can be given:
  • MethodAutomaticmethod to use
    Modulus0integer modulus to use
    ToleranceAutomaticnumerical tolerance to use
    ZeroTestAutomaticfunction to test whether matrix elements should be considered to be zero
  • RowReduce[m,Modulus->n] performs row reduction modulo n. »
  • RowReduce[m,ZeroTest->test] evaluates test[m[[i,j]]] to determine whether matrix elements are zero.
  • Possible settings for the Method option include "CofactorExpansion", "DivisionFreeRowReduction", and "OneStepRowReduction". The default setting of Automatic switches among these methods depending on the matrix given.

Examples

open allclose all

Basic Examples  (3)

Do row reduction on a square matrix:

Do row reduction on a rectangular matrix:

Scope  (2)

m is an exact 4×4 matrix:

Use exact arithmetic for the Gaussian elimination:

With machine‐number arithmetic, the leading zeros and ones are still exact:

With higher‐precision arithmetic, the leading zeros and ones are still exact:

Row reduction for a random complex 3×4 matrix:

Options  (2)

Modulus  (1)

m is a 3×3 matrix of integers between 0 and 4:

Row reduction of m in ordinary arithmetic:

Row reduction of m in arithmetic modulo 5:

Tolerance  (1)

m is an ill-conditioned matrix:

In exact arithmetic, m is clearly non-degenerate:

With machine arithmetic, the default is to consider elements that are too small as zero:

With zero tolerance, even small terms may be taken into account:

With an augmented matrix, you can see how possible solution components are amplified:

Applications  (2)

m is a matrix and b is a vector:

Form an augmented matrix :

Do row reduction on the augmented matrix:

The last column is the solution of :

Do it for another right‐hand side:

There is no solution to since there is a leading 1 in the last column:

m is a symbolic matrix:

Find the symbolic inverse:

This is the equivalent to what is given by Inverse:

Properties & Relations  (3)

m is a non-degenerate square matrix:

RowReduce[m] is IdentityMatrix[Length[m]]:

Augment m with the 3×3 identity matrix:

Do row reduction on the augmented matrix:

The last three columns of the result are Inverse[m]:

m is a 3×5 matrix:

m has its maximal MatrixRank of 3:

The first 3 columns of RowReduce[m] are the 3×3 identity matrix:

m is a degenerate square matrix:

Augment m with the 4×4 identity matrix:

Do row reduction on the augmented matrix:

The last 4 columns of any row with the leading one beyond the 4^(th) column is in the null space:

Even though the vectors are not the same, they are a basis for the same space:

Wolfram Research (1988), RowReduce, Wolfram Language function, https://reference.wolfram.com/language/ref/RowReduce.html (updated 1996).

Text

Wolfram Research (1988), RowReduce, Wolfram Language function, https://reference.wolfram.com/language/ref/RowReduce.html (updated 1996).

BibTeX

@misc{reference.wolfram_2021_rowreduce, author="Wolfram Research", title="{RowReduce}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/RowReduce.html}", note=[Accessed: 23-July-2021 ]}

BibLaTeX

@online{reference.wolfram_2021_rowreduce, organization={Wolfram Research}, title={RowReduce}, year={1996}, url={https://reference.wolfram.com/language/ref/RowReduce.html}, note=[Accessed: 23-July-2021 ]}

CMS

Wolfram Language. 1988. "RowReduce." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/RowReduce.html.

APA

Wolfram Language. (1988). RowReduce. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RowReduce.html