RangeSpace[a]
gives a minimal list of vectors that form a basis for the range space of the matrix a.


RangeSpace
RangeSpace[a]
gives a minimal list of vectors that form a basis for the range space of the matrix a.
Details


- RangeSpace is also known as the range, image, im or column space of a linear transformation.
- The range space of an
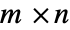 matrix a is the linear space of values, i.e.
matrix a is the linear space of values, i.e. 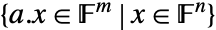 , where
, where 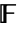 is the field of constants, typically the reals
is the field of constants, typically the reals 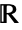 or complexes
or complexes 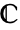 .
. - The returned list of vectors is a basis for the range space
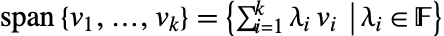 .
. - The dimension of the range space is the length of the returned list of vectors.
- For an
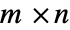 matrix, Length[RangeSpace[a]]+Length[NullSpace[a]]==n, also known as the rank–nullity theorem. »
matrix, Length[RangeSpace[a]]+Length[NullSpace[a]]==n, also known as the rank–nullity theorem. » - RangeSpace works on both numerical and symbolic rectangular matrices.
- The row space
![{y.a|y in F^m}={TemplateBox[{a}, Transpose].y|y in F^m} {y.a|y in F^m}={TemplateBox[{a}, Transpose].y|y in F^m}](Files/RangeSpace.en/8.png) can be computed through RangeSpace[a].
can be computed through RangeSpace[a]. - The following options can be given:
-
Method Automatic method to use Modulus 0 integer modulus to use Tolerance Automatic numerical tolerance to use ZeroTest Automatic function to test whether matrix elements should be considered to be zero - For approximate numeric matrices, SingularValueDecomposition is used, and Tolerance controls the singular values that are taken to be zero.
- For exact numeric and symbolic matrices, RowReduce is used, and Method, Modulus and ZeroTest only apply to this case.
- For symbolic matrices, RangeSpace will treat all unknowns as having generic values. The result can be incorrect for special cases. »
- RangeSpace[m,Modulus->n] finds the range space of rational matrices modulo the integer n. If n is zero, ordinary arithmetic is used. If n is not prime, the computation may fail. »
- RangeSpace[m,ZeroTest->test] evaluates test[m[[i,j]]] to determine whether matrix elements are zero.
- Possible settings for the Method option include "CofactorExpansion", "DivisionFreeRowReduction" and "OneStepRowReduction".
Examples
open all close allBasic Examples (3)
Scope (13)
Basic Uses (8)
Range space of a matrix of rationals:
Range space of a machine-precision matrix:
Range space of a complex matrix:
Range space of an arbitrary-precision matrix:
Range space of an exact matrix:
Find the range space symbolically:
The above result is generic; special values of the symbols may give different results:
Range space of a tall rectangular matrix:
Range space of a wide rectangular matrix:
The range space of a large numerical matrix is computed efficiently:
Special Matrices (5)
Range space of a sparse matrix:
Range space of a structured matrix:
Compute the range space for HilbertMatrix:
Range space of a matrix with finite field elements:
Compute the range space of a 10×12 matrix of univariate polynomials of degree 100:
Options (3)
Modulus (1)
Tolerance (1)
ZeroTest (1)
By default, symbolic expressions are considered nonzero:
In this case, RangeSpace is missing the special case ![]() that produces a singular matrix:
that produces a singular matrix:
Write a function that tests if an expression might be zero:
Pass test[k] as the value of ZeroTest to get a more symbolic reduction:
This gives a valid, if nonstandard, basis for generic values of ![]() :
:
For ![]() , a two-dimensional range space is shown, even if the output includes an extraneous zero vector:
, a two-dimensional range space is shown, even if the output includes an extraneous zero vector:
The extraneous vector can be removed, for example, with DeleteCases:
Applications (17)
The Geometry of RangeSpace (6)
The following matrix has a one-dimensional range space:
Any vector of the form ![]() will lie along the line parallel to
will lie along the line parallel to ![]() :
:
Generate 50 random points in the range space:
Visualize how the points lie along the line generated by ![]() :
:
The following matrix has a two-dimensional range space:
Any vector of the form ![]() will lie in the plane generated by
will lie in the plane generated by ![]() and
and ![]() :
:
Generate 2500 random points in the range space:
Visualize how the points lie on the plane generated by ![]() and
and ![]() :
:
The following matrix has a three-dimensional range space:
Since ![]() is
is ![]() , the range space is all of
, the range space is all of ![]() , and
, and ![]() has a solution for any value of
has a solution for any value of ![]() :
:
Generate 2500 random points in the range space:
Visualize how the points fill a solid region:
The following system of equations has no solution:
Rewrite the system in matrix form:
The range space of the coefficient matrix ![]() is a plane:
is a plane:
The vector ![]() does not lie in this plane, so the system has no solutions:
does not lie in this plane, so the system has no solutions:
The following overdetermined system of equations has a solution:
Rewrite the system in matrix form:
The range space of the coefficient matrix ![]() is a plane:
is a plane:
The vector ![]() lies in this plane, so the system has a solution:
lies in this plane, so the system has a solution:
Create a visualization of the fact that ![]() . Compute a basis for
. Compute a basis for ![]() with RangeSpace:
with RangeSpace:
Compute a basis for ![]() with NullSpace and Transpose:
with NullSpace and Transpose:
Use InfiniteLine and InfinitePlane to visualize the two perpendicular subspaces:
Equation Solving and Invertibility (6)
Determine if the following system of equations has a unique solution:
Rewrite the system in matrix form:
The range space is full dimensional, so the system has a unique solution:
Verify the result using Solve:
Find all values of the ![]() for which the following overdetermined linear system has a solution:
for which the following overdetermined linear system has a solution:
Rewrite the system in matrix form:
Find the range space of the coefficient matrix ![]() :
:
Assign the ![]() to be the components of a general linear combination of basis vectors for the range space:
to be the components of a general linear combination of basis vectors for the range space:
Use Solve to confirm that it is possible to solve for ![]() ,
, ![]() and
and ![]() for every value of the
for every value of the ![]() :
:
Find all values of the vector ![]() for which the equation
for which the equation ![]() has a solution, and the general solution
has a solution, and the general solution ![]() :
:
![]() is a 3×3 singular matrix whose range space is not full dimensional:
is a 3×3 singular matrix whose range space is not full dimensional:
![]() for which there is a solution must be a linear combination of range space basis vectors:
for which there is a solution must be a linear combination of range space basis vectors:
Confirm that there is a solution for each such ![]() by finding one using LinearSolve:
by finding one using LinearSolve:
All solutions are given by ![]() , where
, where ![]() is any vector in the null space:
is any vector in the null space:
Construct the general solution:
Determine if the following matrix has an inverse:
The range space is not full dimensional, so the matrix is not invertible:
Verify the result using Inverse:
Determine if the following matrix has a nonzero determinant:
Since the range space is full dimensional, the matrix must have nonzero determinant:
Confirm the result using Det:
Estimate the fraction of random 10×10 0–1 matrices that are invertible:
Spans and Linear Independence (5)
Find the dimension of the column space of the following matrix:
Column space is just another name for range space, so the answer can be computed directly:
Find the dimension of the subspace spanned by the following vectors:
By definition, this is the dimension of the range space of the matrix whose columns are the vectors:
The following three vectors are not linearly independent:
Find the range space of the matrix whose columns are the vectors:
The dimension of the range space is less than the number of vectors because of the linear dependence:
The following three vectors are linearly independent:
Find the range space of the matrix whose columns are the vectors:
The dimension of the range space equals the number of vectors because of the linear independence:
Determine if the following vectors are linearly independent or not:
The range space of ![]() is less than four dimensional, so they are not linearly independent:
is less than four dimensional, so they are not linearly independent:
Properties & Relations (13)
RangeSpace[m] is spanned by nonzero vectors of the echelon form of Transpose[m]:
RowReduce gives the echelon form, including zero vectors:
The dimension of the range space is the rank of the matrix:
The sum of the dimensions of RangeSpace[m] and NullSpace[m] equals the number of columns of m (the rank-nullity theorem):
If m is exact, each element of RangeSpace[m] will have a 1 as its first nonzero entry:
If m is inexact, there are no constraints on the form of the elements:
For any two compatible matrices a and b, RangeSpace[a.b] is contained in RangeSpace[a]:
For these particular matrices, RangeSpace[a.b] is a lower-dimensional subspace:
However, for any real-valued matrix, the range spaces of a and a.Transpose[a] are the same:
For any matrix, the range spaces of a and a.ConjugateTranspose[a] are the same:
RangeSpace[a] is orthogonal NullSpace[ConjugateTranspose[a]]:
For real-valued matrices, the latter space can be taken to be NullSpace[Transpose[a]]:
For a square matrix, m has a full-dimensional range space if and only if Det[m]!=0:
For a square matrix, m has a full-dimensional range space if and only if m has full rank:
For a square matrix, m has a full-dimensional range space if and only if m has an inverse:
For a square matrix, m has a trivial null space iff LinearSolve[m,b] has a solution for a generic b:
The range space of a square matrix m can be computed using SingularValueDecomposition:
Do row reduction on the transposed matrix:
The nonzero columns of u.σ—here, the first two, due to the zeros in σ—are a basis for the range space:
Get the vectors using RangeSpace:
Even though the vectors are not the same, they are a basis for the same vector subspace:
Related Guides
History
Text
Wolfram Research (2025), RangeSpace, Wolfram Language function, https://reference.wolfram.com/language/ref/RangeSpace.html.
CMS
Wolfram Language. 2025. "RangeSpace." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RangeSpace.html.
APA
Wolfram Language. (2025). RangeSpace. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RangeSpace.html
BibTeX
@misc{reference.wolfram_2025_rangespace, author="Wolfram Research", title="{RangeSpace}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/RangeSpace.html}", note=[Accessed: 16-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_rangespace, organization={Wolfram Research}, title={RangeSpace}, year={2025}, url={https://reference.wolfram.com/language/ref/RangeSpace.html}, note=[Accessed: 16-January-2026]}