InfinitePlane[{p1,p2,p3}]
represents the plane passing through the points p1, p2, and p3.
InfinitePlane[p,{v1,v2}]
represents the plane passing through the point p in the directions v1 and v2.


InfinitePlane
InfinitePlane[{p1,p2,p3}]
represents the plane passing through the points p1, p2, and p3.
InfinitePlane[p,{v1,v2}]
represents the plane passing through the point p in the directions v1 and v2.
Details

- InfinitePlane is also known as plane or hyperplane.
- InfinitePlane can be used as a geometric region and graphics primitive.
- InfinitePlane represents a plane
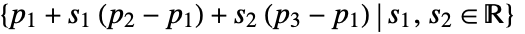 or
or 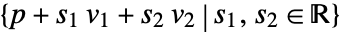 .
. - Hyperplane[n,p] is an alternative representation using a normal n in 3D.
- InfinitePlane can be used in Graphics and Graphics3D.
- InfinitePlane will be clipped by PlotRange when rendering.
- In graphics, the points p, pi and vector v can be Dynamic expressions.
- Graphics rendering is affected by directives such as FaceForm, Opacity, and color.
- FaceForm[front,back] can be used to specify different styles for the front and back in 3D. The front is defined by the right-hand rule and the direction of the points pi or the vectors vi.
- InfinitePlane can be used with functions such as RegionMeasure, RegionCentroid, etc.
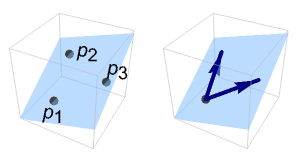
Examples
open all close allBasic Examples (3)
An InfinitePlane in 3D:
Scope (17)
Graphics (7)
Specification (2)
Styling (2)
Coordinates (3)
Specify coordinates by fractions of the plot range:
Specify scaled offsets from the ordinary coordinates:
Points and vectors can be Dynamic:
Regions (10)
Embedding dimension is the dimension of the coordinates:
Geometric dimension is the dimension of the region itself:
Get the conditions for membership:
An infinite plane has infinite measure and undefined centroid:
An infinite plane is unbounded:
Integrate over an infinite plane:
Applications (7)
Find the plane in which a triangle is embedded:
InfinitePlane can use the same parametrization as Triangle:
Find the plane in which a polygon is embedded:
To find the plane, take the first three points (or any three points not on a line):
The tangent plane to a parametric surface f[u,v] is given by InfinitePlane[f[u,v],{∂uf[u,v],∂vf[u,v]}]. Find the tangent plane to the parametric surface ![]() :
:
Find the tangent plane to the surface ![]() :
:
Find the intersection points of a sphere, a plane, and a surface defined by ![]() :
:
Visualize intersection points:
Partition space in a BubbleChart:
Define a ReflectionTransform using a point on the plane and its normal vector:
Properties & Relations (6)
InfinitePlane[{p1,p2,p3}] is equivalent to InfinitePlane[p1,{p2-p1,p3-p1}]:
InfinitePlane[p,{v1,v2}] is equivalent to Hyperplane[Cross[v1,v2],p] in 3D:
ParametricRegion can represent any InfinitePlane:
ImplicitRegion can represent any InfinitePlane:
InfinitePlane is a special case of ConicHullRegion:
Any InfinitePlane can be represented as a union of two HalfPlane regions:
See Also
HalfPlane Hyperplane Polygon InfiniteLine HalfLine ConicHullRegion
Function Repository: HessianPlane
Related Guides
Text
Wolfram Research (2014), InfinitePlane, Wolfram Language function, https://reference.wolfram.com/language/ref/InfinitePlane.html (updated 2016).
CMS
Wolfram Language. 2014. "InfinitePlane." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/InfinitePlane.html.
APA
Wolfram Language. (2014). InfinitePlane. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InfinitePlane.html
BibTeX
@misc{reference.wolfram_2025_infiniteplane, author="Wolfram Research", title="{InfinitePlane}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/InfinitePlane.html}", note=[Accessed: 16-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_infiniteplane, organization={Wolfram Research}, title={InfinitePlane}, year={2016}, url={https://reference.wolfram.com/language/ref/InfinitePlane.html}, note=[Accessed: 16-January-2026]}