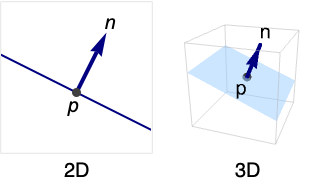
Hyperplane

Hyperplane[n,p]

represents the hyperplane with normal n passing through the point p.

Hyperplane[n,c]

represents the hyperplane with normal n given by the points that satisfy .

Details

Hyperplane can be used as a geometric region and a graphics primitive.
Hyperplane[n] is equivalent to Hyperplane[n,0], a hyperplane through the origin.
Hyperplane corresponds to an infinite line in 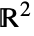and an infinite plane in .

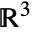Hyperplane represents the set 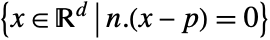or .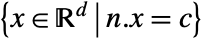
Hyperplane is defined for n∈^d, p∈^d, and c∈.
Hyperplane can be used in Graphics and Graphics3D.
Hyperplane will be clipped by PlotRange when rendering.
Graphics rendering is affected by directives such as Thickness, Dashing, Opacity, and color.
Graphics3D rendering is affected by directives such as Opacity and color. FaceForm[front,back] can be used to specify different styles for the front and back, where front is defined to be in the direction of the normal n.

Examples

open allclose all

Basic Examples (3)

A Hyperplane in 2D:

And in 3D:

Different styles applied to a hyperplane region:

Determine if points belong to a given hyperplane region:

Scope (15)

Graphics (5)

Specification (2)

A hyperplane in 2D defined by a normal vector and a point:

The same hyperplane defined by a normal vector and a constant:

Define a hyperplane in 3D using a normal vector and a point:

Define the same hyperplane using a normal vector and a constant:

Hyperplanes varying in direction of the normal:

Styling (2)

Color directives specify the color of the hyperplane:

FaceForm and EdgeForm can be used to specify the styles of the faces and edges:

Coordinates (1)

Points and vectors can be Dynamic:

Regions (10)

Embedding dimension is the dimension of the coordinates:

Geometric dimension is the dimension of the region itself:

Point membership test:

Get the conditions for membership:

A hyperplane has infinite measure and undefined centroid:

Distance from a point:

Signed distance from a point:

Nearest point in the region:

Nearest points:

A hyperplane is unbounded:

Find the region range:

In the axis-aligned case, it is bounded in some directions:

Integrate over a hyperplane:

Optimize over a hyperplane:

Solve equations over a hyperplane:

Applications (11)

Hyperplane Arrangements (7)

In a parallel arrangement of hyperplanes, all hyperplanes have the same normal n:

Orthogonal arrangements of hyperplanes:

Grids of hyperplanes:

Random arrangements of hyperplanes:

A pencil of hyperplanes is all hyperplanes through a point:

A sheaf of hyperplanes is all hyperplanes through a line:

A bundle of hyperplanes, where all pass through a common point:

Tangent Planes (4)

A tangent plane to an implicitly defined curve in 2D is given by its normal at a point on the curve. Start by finding points on the curve:

Find tangent lines at each of the points:

Visualize the solution:

A tangent plane to an implicitly defined surface in 3D is also given by its normal and a point on the surface. Start by finding points on the surface: