HalfPlane

HalfPlane[{p1,p2},w]

represents the half-plane bounded by the line through p1 and p2 and extended in the direction w.

HalfPlane[p,v,w]

represents the half-plane bounded by the line through p along v and extended in the direction w.

Details

  • HalfPlane is also known as half-space in 2D.
  • HalfPlane can be used as a geometric region and graphics primitive.
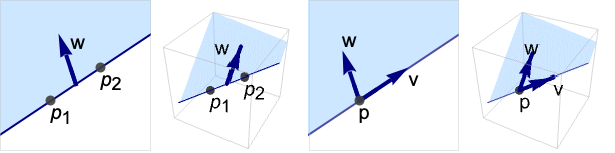
  • HalfPlane represents a planar region 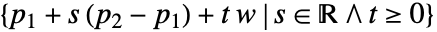or .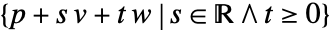
  • HalfPlane can be used in Graphics and Graphics3D.
  • HalfPlane will be clipped by PlotRange when rendering.
  • In graphics, the points p, pi and vector v can be Scaled and Dynamic expressions.
  • Graphics rendering is affected by directives such as FaceForm, EdgeForm, Opacity, and color.
  • FaceForm[front,back] can be used to specify different styles for the front and back in 3D. The front is defined by the right-hand rule and the direction from {p1,w,p2} or {p,v,w}.

Examples

open allclose all

Basic Examples  (4)

A HalfPlane in 2D:

And in 3D:

Different styles applied to a half-plane:

The Area of a half-plane is infinite:

Determine if points belong to a given half-plane:

Scope  (18)

Graphics  (8)

Specification  (3)

Define the upper half-plane using a point and two vectors:

Or using two points and a single vector:

Define a half-plane in 3D using a point and two vectors:

Or using two points and a single vector:

A half-plane with symbolic parameters:

Styling  (2)

Color directives specify the color of the half-plane:

FaceForm and EdgeForm can be used to specify the styles of the faces and edges:

Coordinates  (3)

Specify coordinates by fractions of the plot range:

Specify scaled offsets from the ordinary coordinates in 2D:

Points and vectors can be Dynamic:

Regions  (10)

Embedding dimension is the dimension of the coordinates:

Geometric dimension is the dimension of the region itself:

Membership testing:

Get conditions for membership:

Half-planes have infinite measure and undefined centroid:

Distance from a point to a half-plane:

Visualizing it:

Signed distance to a half-plane:

Plotting it:

Nearest point:

Visualize it:

A half-plane is unbounded:

Find the region range:

Integrate over a half-plane:

Optimize over a half-plane:

Solve equations over a half-plane:

Applications  (3)

Define regions that occupy two adjacent quadrants:

Partition space in a BubbleChart:

Combine the graphics:

Find the intersection points of a sphere, a half-plane, and a surface defined by :

Visualize intersection points:

Properties & Relations  (4)

Any HalfPlane can be represented by ConicHullRegion:

ImplicitRegion can be used to represent any HalfPlane:

ParametricRegion can be used to represent any HalfPlane:

Any InfinitePlane can be represented as a union of two half-planes:

Neat Examples  (1)

A collection of random half-planes:

Wolfram Research (2014), HalfPlane, Wolfram Language function, https://reference.wolfram.com/language/ref/HalfPlane.html (updated 2016).

Text

Wolfram Research (2014), HalfPlane, Wolfram Language function, https://reference.wolfram.com/language/ref/HalfPlane.html (updated 2016).

CMS

Wolfram Language. 2014. "HalfPlane." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/HalfPlane.html.

APA

Wolfram Language. (2014). HalfPlane. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HalfPlane.html

BibTeX

@misc{reference.wolfram_2024_halfplane, author="Wolfram Research", title="{HalfPlane}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/HalfPlane.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_halfplane, organization={Wolfram Research}, title={HalfPlane}, year={2016}, url={https://reference.wolfram.com/language/ref/HalfPlane.html}, note=[Accessed: 21-December-2024 ]}