Abs[z]
gives the absolute value of the real or complex number z.


Abs
Abs[z]
gives the absolute value of the real or complex number z.
Details
- Abs is also known as modulus.
- Mathematical function, suitable for both symbolic and numerical manipulation.
- For complex numbers z, Abs[z] gives the modulus
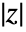 .
. - Abs[z] is left unevaluated if z is not a numeric quantity.
- Abs automatically threads over lists. »
- Abs can be used with Interval and CenteredInterval objects. »
Examples
open all close allBasic Examples (4)
Scope (34)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
Compute the elementwise values of an array using automatic threading:
Or compute the matrix Abs function using MatrixFunction:
Abs can be used with Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Specific Values (6)
Values of Abs at fixed points:
Find real values of ![]() for which
for which ![]() :
:
Visualization (5)
Function Properties (11)
Abs is defined for all real and complex inputs:
The range of Abs is the non-negative reals:
This is true even in the complex plane:
Abs is an even function:
Abs is not a differentiable function:
The difference quotient does not have a limit in the complex plane:
There is only a limit in certain directions, for example, the real direction:
This result, restricted to real inputs, is the derivative of RealAbs:
Abs is not an analytic function:
It has singularities but no discontinuities:
Over the complex plane, it is singular everywhere but still continuous:
Abs is neither nondecreasing nor nonincreasing:
Abs is not injective:
Abs is not surjective:
Abs is non-negative:
Abs is convex:
TraditionalForm formatting:
Function Identities and Simplifications (6)
Expand assuming real variables x and y:
Simplify Abs using appropriate assumptions:
Express a complex number as a product of Abs and Sign:
Express in terms of real and imaginary parts:
Abs commutes with real exponentiation:
This result is applied automatically for concrete powers:
Find the absolute value of a Root expression:
Properties & Relations (16)
Abs is idempotent:
Abs is defined for all complex numbers:
RealAbs is defined only for real numbers:
Simplify expressions containing Abs:
Simplification of some identities involving Abs may require explicit assumptions that variables are real:
The assumptions may not be needed if RealAbs is used instead:
Abs is not a differentiable function:
RealAbs is differentiable:
Use Abs as a target function in ComplexExpand:
Solve an equation involving Abs:
Prove an inequality containing Abs:
Integrate along a line in the complex plane, symbolically and numerically:
Interpret as the indefinite integral for real arguments:
Convert into Piecewise:
ComplexPlot3D plots the magnitude of a function as height and colors using the phase:
Possible Issues (3)
Abs is a function of a complex variable and is therefore not differentiable:
As a complex function, it is not possible to write Abs[z] without involving Conjugate[z]:
In particular, the limit that defines the derivative is direction dependent and therefore does not exist:
Adding assumptions that the argument is real makes Abs differentiable:
Alternatively, use RealAbs, which assumes its argument is real:
Abs can stay unevaluated for some complicated numeric arguments:
No series can be formed from Abs for complex arguments:
Tech Notes
History
Introduced in 1988 (1.0) | Updated in 2021 (13.0)
Text
Wolfram Research (1988), Abs, Wolfram Language function, https://reference.wolfram.com/language/ref/Abs.html (updated 2021).
CMS
Wolfram Language. 1988. "Abs." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Abs.html.
APA
Wolfram Language. (1988). Abs. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Abs.html
BibTeX
@misc{reference.wolfram_2025_abs, author="Wolfram Research", title="{Abs}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Abs.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_abs, organization={Wolfram Research}, title={Abs}, year={2021}, url={https://reference.wolfram.com/language/ref/Abs.html}, note=[Accessed: 09-March-2026]}