StirlingS2

StirlingS2[n,m]

gives the Stirling number of the second kind .

Details

  • Integer mathematical function, suitable for both symbolic and numerical manipulation.
  • StirlingS2 is defined as the conversion matrix from Power of continuous calculus to FactorialPower of discrete calculus x^n=sum_(m=1)^n TemplateBox[{n, m}, StirlingS2]TemplateBox[{x, m}, FactorialPower], where m,n in TemplateBox[{}, PositiveIntegers].
  • gives the number of ways of partitioning a set of 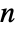elements into 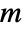non‐empty subsets.
  • StirlingS2 automatically threads over lists.

Examples

open allclose all

Basic Examples  (1)

Scope  (2)

StirlingS2 threads element-wise over lists:

TraditionalForm formatting:

Applications  (4)

Plot Stirling numbers of the second kind on a logarithmic scale:

Stirling numbers modulo 2:

Closed form of derivatives of compositions with exponential functions:

A fair ‐sided die is thrown times independently. The probability that all faces appear at least once is given in terms of Stirling numbers of the second kind:

Plot the probability for a six-sided die:

Check with simulations:

Properties & Relations  (6)

Generate values from the generating function:

Stirling numbers of the second kind are effectively inverses of Stirling numbers of the first kind:

Calculate large Stirling numbers of the second kind using Cauchy's theorem:

Generate Stirling numbers of the second kind from the commutation relation :

The limit of finite differences of powers are Stirling numbers of the second kind:

Stirling numbers of the second kind are given by a partial Bell polynomial with unit arguments:

Possible Issues  (2)

StirlingS2 can take large values for moderate‐size arguments:

The value at is defined to be 1:

Neat Examples  (2)

Plot sums of digits:

Wolfram Research (1988), StirlingS2, Wolfram Language function, https://reference.wolfram.com/language/ref/StirlingS2.html.

Text

Wolfram Research (1988), StirlingS2, Wolfram Language function, https://reference.wolfram.com/language/ref/StirlingS2.html.

CMS

Wolfram Language. 1988. "StirlingS2." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StirlingS2.html.

APA

Wolfram Language. (1988). StirlingS2. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StirlingS2.html

BibTeX

@misc{reference.wolfram_2023_stirlings2, author="Wolfram Research", title="{StirlingS2}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/StirlingS2.html}", note=[Accessed: 22-September-2023 ]}

BibLaTeX

@online{reference.wolfram_2023_stirlings2, organization={Wolfram Research}, title={StirlingS2}, year={1988}, url={https://reference.wolfram.com/language/ref/StirlingS2.html}, note=[Accessed: 22-September-2023 ]}