BellB

BellB[n]

gives the Bell number TemplateBox[{n}, BellB].

BellB[n,x]

gives the Bell polynomial TemplateBox[{n, x}, BellB2].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • The Bell polynomials satisfy the generating function relation e^((e^t-1)x)=sum_(n=0)^(infty)(TemplateBox[{n, x}, BellB2]t^n)/(n!).
  • The Bell numbers are given by TemplateBox[{n}, BellB]=TemplateBox[{n, 1}, BellB2].
  • For certain special arguments, BellB automatically evaluates to exact values.
  • BellB can be evaluated to arbitrary numerical precision.
  • BellB automatically threads over lists.

Background & Context

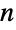
  • BellB is a mathematical function that returns a Bell number or polynomial. In particular, BellB[n,x] returns the 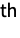^(th) Bell polynomial 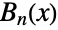and BellB[n] returns the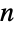 ^(th) Bell number TemplateBox[{n}, BellB]=TemplateBox[{n, 1}, BellB2]. Bell polynomials can be determined from the exponential generating function 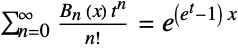. The Bell numbers also satisfy the recurrence relation B_(n+1)=sum_(k=0)^nTemplateBox[{n, k}, Binomial]B_k. The first few Bell polynomials are 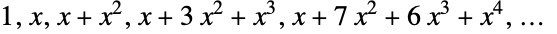, while the first few Bell numbers 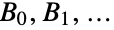are .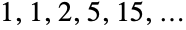
  • The Bell polynomial is also called an exponential polynomial or, more explicitly, the "complete exponential Bell polynomial" and is sometimes denoted 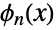. Bell polynomials are named after mathematician and math expositor Eric Temple Bell, who wrote about them in 1934.
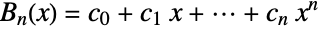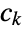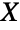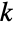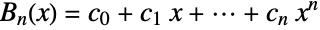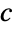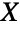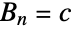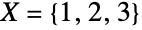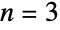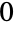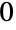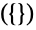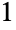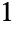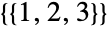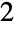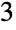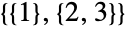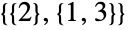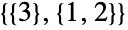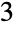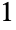  • The polynomial has the interpretation that if there are partitions of into parts, then . Furthermore, if there are total partitions of , then . For example, the set having elements can be partitioned into parts ways , part way (), parts ways (, and ), and parts way (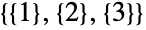), giving 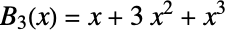. Since there are five total ways to partition , .
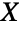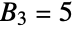  • The Bell polynomial and number are a special case of the BellY function, with TemplateBox[{n, x}, BellB2]=sum_(k=0)^nY_(n,k)(x,...,x) and 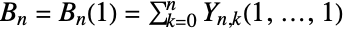. Letting TemplateBox[{n, k}, StirlingS2] denote the Stirling number of the second kind, returned by StirlingS2, B_n=B_n(1)=sum_(k=0)^nTemplateBox[{n, k}, StirlingS2].

Examples

open allclose all

Basic Examples  (2)

The tenth Bell number:

The fifth Bell polynomial:

Scope  (5)

Evaluate numerically:

The precision of the output tracks the precision of the input:

BellB threads element-wise over lists:

BellB can be applied to a power series:

TraditionalForm formatting:

Applications  (4)

BellB numbers versus their asymptotics:

Compute the first 10 complementary Bell numbers:

Compare with an expression in terms of the Stirling number of the second kind:

Verify an expression for the Bell number in terms of a Hessenberg determinant for the first few cases:

The Bell numbers BellB[n] can be characterized as the unique set of numbers such that two certain Hankel determinants made from these numbers are both equal to BarnesG[n+2]. Verify for the first few cases:

Properties & Relations  (7)

The exponential generating function for BellB:

Compare with the explicit summation formula:

Sum can give results involving BellB:

The ^(th) moment of a PoissonDistribution is given by the ^(th) Bell polynomial in its mean :

Use FullSimplify to simplify expressions involving BellB:

Compute Bell numbers directly from set partitions :

Use IntegerPartitions to directly sum over terms that satisfy the constraints on indices:

Compare with the result of BellB:

Compute Bell numbers using generalized Bell polynomials:

Compute Bell polynomials using generalized Bell polynomials:

FindSequenceFunction can recognize the BellB sequence:

Possible Issues  (1)

The first argument of BellB must be a non-negative integer:

Neat Examples  (1)

Integral representation for Bell numbers by Cesàro:

Wolfram Research (2007), BellB, Wolfram Language function, https://reference.wolfram.com/language/ref/BellB.html.

Text

Wolfram Research (2007), BellB, Wolfram Language function, https://reference.wolfram.com/language/ref/BellB.html.

CMS

Wolfram Language. 2007. "BellB." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BellB.html.

APA

Wolfram Language. (2007). BellB. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BellB.html

BibTeX

@misc{reference.wolfram_2025_bellb, author="Wolfram Research", title="{BellB}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/BellB.html}", note=[Accessed: 25-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_bellb, organization={Wolfram Research}, title={BellB}, year={2007}, url={https://reference.wolfram.com/language/ref/BellB.html}, note=[Accessed: 25-May-2025 ]}