BellY

BellY[n,k,{x1,…,xn-k+1}]

gives the partial Bell polynomial TemplateBox[{n, k, {x, _, 1}, ..., {x, _, {(, {n, -, k, +, 1}, )}}}, BellY].

BellY[n,k,m]

gives the generalized partial Bell polynomial of a matrix m.

BellY[m]

gives the generalized Bell polynomial of a matrix m.

Details

  • Mathematical function, suitable for both symbolic and numeric manipulations.
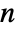
  • The partial Bell polynomial can be used to express the 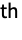^(th) derivative of a composition of two functions through the Faà di Bruno formula D_t^nf(g(t))=sum_(k=0)^nf^((k))(g(t)) TemplateBox[{n, k, {{g, ^, {(, ', )}}, (, t, )}, {{g, ^, {(, '', )}}, (, t, )}, ..., {{g, ^, {(, {(, {n, -, k, +, 1}, )}, )}}, (, t, )}}, BellY]. »
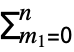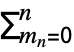
  • The BellY polynomial TemplateBox[{n, k, {x, _, 1}, ..., {x, _, {(, {n, -, k, +, 1}, )}}}, BellY] is given by ⋯ 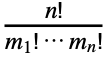Boole[m1+2 m2+⋯+n mnn∧m1+m2+⋯+mnk] 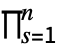(xs/s!)ms. »
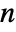
  • The generalized Bell polynomial can be used to express the ^(th) derivative of a composition of 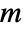functions D_t^nf_1(f_2(...f_m(t)...))⩵TemplateBox[{{{{{{f, _, 1}, '}, {(, {{f, _, 2}, (, {..., , {{f, _, m}, (, t, )}, ...}, )}, )}}, , {{{f, _, 2}, '}, {(, {{f, _, 3}, (, {..., , {{f, _, m}, (, t, )}, ...}, )}, )}}, , ..., , {{{f, _, m}, '}, {(, t, )}}}, ; , {{{{f, _, 1}, ''}, {(, {{f, _, 2}, (, {..., , {{f, _, m}, (, t, )}, ...}, )}, )}}, , {{{f, _, 2}, ''}, {(, {{f, _, 3}, {(, {..., , {{f, _, m}, (, t, )}, ...}, )}}, )}}, , ..., , {{{f, _, m}, ''}, {(, t, )}}}, ; , {|, , |, , ..., , |}, ; , {{{{f, _, 1}, ^, {(, {(, n, )}, )}}, (, {{f, _, 2}, (, {..., , {{f, _, m}, (, t, )}, ...}, )}, )}, , {{{f, _, 2}, ^, {(, {(, n, )}, )}}, (, {{f, _, 3}, (, {..., , {{f, _, m}, (, t, )}, ...}, )}, )}, , ..., , {{{f, _, m}, ^, {(, {(, n, )}, )}}, (, t, )}}}}, BellY1].
  • BellY[n,k,m] is equivalent to BellY[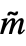] where 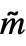is formed by prepending UnitVector[n,k] to m as a first column. »

Examples

open allclose all

Basic Examples  (3)

Partial Bell polynomial:

Generalized partial Bell polynomial:

Generalized Bell polynomial:

Scope  (1)

Evaluate for a numerical matrix:

Applications  (13)

Calculus  (3)

The generalized chain rule allows one to directly compute the ^(th) derivative of using BellY: (partial^nf(g(x)))/(partialx^n)=sum_(k=1)^nf^((k))(g(x)) TemplateBox[{n, k, {{(, {partial, {g, (, x, )}}, )}, /, {(, {partial, {x, ^, 1}}, )}}, ..., {{(, {{partial, ^, {(, {n, -, k, +, 1}, )}}, {g, (, x, )}}, )}, /, {(, {partial, {x, ^, {(, {n, -, k, +, 1}, )}}}, )}}}, BellY]. Verify this with symbolic and for low orders of :

For , this becomes the normal chain rule:

For , this is also known as Faà di Bruno's formula:

From the formula, it can be directly seen that the derivative is linear in with coefficients that are polynomial in , where TemplateBox[{n, k, {g, ^, {(, ', )}}, ..., {g, ^, {(, {(, {{-, k}, +, n, +, 1}, )}, )}}}, BellY] is the polynomial coefficient of . Define a typesetting rule that makes this relation obvious by paneling the Bell coefficients:

A few of the first derivatives:

Compute fourth-order derivatives of the Gamma function using the BellY polynomial:

Compare with the explicit evaluation of the derivative:

Compute the series of an inverse function:

Compare with the result of InverseSeries:

Combinatorics  (6)

Compute Stirling numbers of the first kind in terms of the partial Bell polynomials:

Compute Stirling numbers of the second kind in terms of the partial Bell polynomials:

Compute Bell numbers using generalized Bell polynomials:

Compute Bell polynomials BellB[n,z] using generalized Bell polynomials:

Compute Catalan numbers using generalized Bell polynomials:

Number of -level labeled rooted trees with leaves:

Compare with an alternative formula:

The cycle index polynomial of the symmetric group of degree n:

Compare with the result of CycleIndexPolynomial:

The cycle index polynomial of the alternating group of degree n:

Compare with the result of CycleIndexPolynomial:

Find the number of ways to partition a set of 6 elements into two subsets from a partial Bell polynomial:

Check by explicit recursive generation of set partitions:

There are 10 ways to partition a set of 6 elements into two subsets of 3+3 elements:

There are 15 ways to partition a set of 6 elements into two subsets of 4+2 elements:

There are 6 ways to partition a set of 6 elements into two subsets of 5+1 elements:

Other Applications  (4)

Define the complete Bell polynomial of n variables:

Show the first few complete Bell polynomials:

Compute the third raw moment in terms of cumulants:

Compute the third cumulant in terms of raw moments:

Construct polynomial sequences of binomial type:

Verify their defining identity:

Recover BellB[n,z] as a special case:

The n^(th) elementary symmetric polynomial can be defined in terms of BellY:

Compare with SymmetricPolynomial for the case of five variables:

Properties & Relations  (6)

Compute a partial Bell polynomial using its sum representation:

Compare with BellY:

Compute a partial Bell polynomial using Cvijović's iterated sum formula:

Compare with BellY:

A linear combination of partial Bell polynomials:

The equivalent expression in terms of the generalized Bell polynomial:

A generalized partial Bell polynomial of a matrix:

This can be computed in terms of the generalized Bell polynomial by prepending a unit vector as a column:

A linear combination of generalized partial Bell polynomials of a matrix can be expressed as a generalized Bell polynomial by prepending the column of coefficients to the matrix:

Faà di Bruno's formula for the third derivative of :

Demonstrate an inversion relation for generalized Bell polynomials:

Neat Examples  (2)

Generate Bernoulli numbers using a generalized Bell polynomial:

Generate Euler numbers using a generalized Bell polynomial:

Wolfram Research (2010), BellY, Wolfram Language function, https://reference.wolfram.com/language/ref/BellY.html.

Text

Wolfram Research (2010), BellY, Wolfram Language function, https://reference.wolfram.com/language/ref/BellY.html.

CMS

Wolfram Language. 2010. "BellY." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BellY.html.

APA

Wolfram Language. (2010). BellY. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BellY.html

BibTeX

@misc{reference.wolfram_2025_belly, author="Wolfram Research", title="{BellY}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/BellY.html}", note=[Accessed: 04-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_belly, organization={Wolfram Research}, title={BellY}, year={2010}, url={https://reference.wolfram.com/language/ref/BellY.html}, note=[Accessed: 04-May-2025 ]}