SymmetricPolynomial[k,{x1,…,xn}]
gives the k![]() elementary symmetric polynomial in the variables x1,…,xn.
elementary symmetric polynomial in the variables x1,…,xn.


SymmetricPolynomial
SymmetricPolynomial[k,{x1,…,xn}]
gives the k![]() elementary symmetric polynomial in the variables x1,…,xn.
elementary symmetric polynomial in the variables x1,…,xn.
Details
- A symmetric polynomial of n variables {x1,…,xn} is invariant under any permutation of its variables. The k
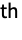 elementary symmetric polynomial is the sum of all square-free monomials of degree k.
elementary symmetric polynomial is the sum of all square-free monomials of degree k. - The degree k must satisfy 0≤k≤n.
- The elementary symmetric polynomials form a basis for the symmetric polynomials.
- Expressing a general symmetric polynomial in terms of elementary symmetric polynomials is accomplished by using SymmetricReduction.
Examples
open all close allApplications (1)
The 2×3 matrices with entries 0 or 1:
Select matrices whose column sums are 1,1,1 and whose row sums are 2,1:
You can also count how many such matrices there are by using SymmetricPolynomial. The generating function of 2×3 matrices whose row sums are 2,1 is given by:
The coefficient of x11x21x31 counts how many of these matrices have column sums 1,1,1:
Properties & Relations (5)
The k![]() elementary symmetric polynomial is the sum of all monomials constructed from k-subsets of the variables:
elementary symmetric polynomial is the sum of all monomials constructed from k-subsets of the variables:
The generating function for the symmetric polynomials in ![]() variables is given by
variables is given by ![]() :
:
The monic polynomial with roots ![]() has coefficients that are elementary symmetric polynomials of the
has coefficients that are elementary symmetric polynomials of the ![]() :
:
The elementary symmetric polynomials ek=SymmetricPolynomial[k,{x1,…,xn}] are related to the power sum polynomials ![]() through the Newton–Girard formulas [MathWorld]. Generate all the Newton–Girard formulas for
through the Newton–Girard formulas [MathWorld]. Generate all the Newton–Girard formulas for ![]() :
:
The elementary symmetric polynomials can be defined in terms of the generalized Bell polynomial BellY:
Tech Notes
Related Guides
History
Text
Wolfram Research (2007), SymmetricPolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/SymmetricPolynomial.html.
CMS
Wolfram Language. 2007. "SymmetricPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SymmetricPolynomial.html.
APA
Wolfram Language. (2007). SymmetricPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SymmetricPolynomial.html
BibTeX
@misc{reference.wolfram_2025_symmetricpolynomial, author="Wolfram Research", title="{SymmetricPolynomial}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/SymmetricPolynomial.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_symmetricpolynomial, organization={Wolfram Research}, title={SymmetricPolynomial}, year={2007}, url={https://reference.wolfram.com/language/ref/SymmetricPolynomial.html}, note=[Accessed: 25-January-2026]}