represents a formal power symmetric polynomial with exponent r.
PowerSymmetricPolynomial[{r1,r2,…}]
represents a multivariate formal power symmetric polynomial with exponents r1, r2, ….
PowerSymmetricPolynomial[rspec,data]
gives the power symmetric polynomial in data.


PowerSymmetricPolynomial
represents a formal power symmetric polynomial with exponent r.
PowerSymmetricPolynomial[{r1,r2,…}]
represents a multivariate formal power symmetric polynomial with exponents r1, r2, ….
PowerSymmetricPolynomial[rspec,data]
gives the power symmetric polynomial in data.
Details
- PowerSymmetricPolynomial[r,{x1,x2,…,xn}] is given by
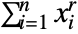 .
. - PowerSymmetricPolynomial[{r1,r2,…},{{x11,x12,…},…,{xn 1,xn 2,…}}] is given by
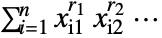 .
. - PowerSymmetricPolynomial[rspec] can be used to represent formal power sums used in moment estimators.
- MomentConvert can be used to generate moment estimators in terms of PowerSymmetricPolynomial objects.
- MomentEvaluate can be used to evaluate polynomials of formal PowerSymmetricPolynomial objects on a dataset.
Examples
open all close allBasic Examples (1)
Scope (3)
PowerSymmetricPolynomial of order 0 is effectively the number of data points:
Use MomentEvaluate to evaluate formal power symmetric polynomials on data:
TraditionalForm formatting:
Applications (1)
Linearize power symmetric polynomials using AugmentedSymmetricPolynomial:
Properties & Relations (1)
PowerSymmetricPolynomial is equivalent to AugmentedSymmetricPolynomial with a single exponent:
This relationship also holds for the multivariate generalization:
Related Guides
History
Text
Wolfram Research (2010), PowerSymmetricPolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/PowerSymmetricPolynomial.html.
CMS
Wolfram Language. 2010. "PowerSymmetricPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PowerSymmetricPolynomial.html.
APA
Wolfram Language. (2010). PowerSymmetricPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PowerSymmetricPolynomial.html
BibTeX
@misc{reference.wolfram_2025_powersymmetricpolynomial, author="Wolfram Research", title="{PowerSymmetricPolynomial}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PowerSymmetricPolynomial.html}", note=[Accessed: 26-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_powersymmetricpolynomial, organization={Wolfram Research}, title={PowerSymmetricPolynomial}, year={2010}, url={https://reference.wolfram.com/language/ref/PowerSymmetricPolynomial.html}, note=[Accessed: 26-February-2026]}