MomentConvert[mexpr,form]
converts the moment expression mexpr to the specified form.




MomentConvert
MomentConvert[mexpr,form]
converts the moment expression mexpr to the specified form.
Details



- MomentConvert handles both formal moment and formal sample moment expressions.
- A formal moment expression can be any polynomial in formal moments of the form:
-
Moment[r] formal r 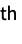 moment
momentCentralMoment[r] formal r 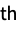 central moment
central momentFactorialMoment[r] formal r 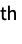 factorial moment
factorial momentCumulant[r] formal r 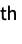 cumulant
cumulant - Formal moment expressions can be evaluated for any particular distribution using MomentEvaluate.
- A moment expression can be converted into any other moment expression.
- The following forms can used for converting between moment expressions:
-
"Moment" convert to formal moments "CentralMoment" convert to formal central moments "FactorialMoment" convert to formal factorial moments "Cumulant" convert to formal cumulants - A sample moment expression is any polynomial in formal symmetric polynomials of the form:
-
PowerSymmetricPolynomial[r] formal r 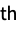 power symmetric polynomial
power symmetric polynomialAugmentedSymmetricPolynomial[{r1,r2,…}] formal {r1,r2,…} augmented symmetric polynomial - Sample moment expressions can be evaluated on a dataset using MomentEvaluate.
- A sample moment expression can be converted into any other sample moment expression.
- The following forms can used for converting between sample moment expressions:
-
"PowerSymmetricPolynomial" convert to formal power symmetric polynomial "AugmentedSymmetricPolynomial" convert to formal augmented symmetric polynomial - Sample moment expressions are effectively moment estimators assuming independent, identically distributed samples.
- Moment estimators for a given moment expression can be constructed using the forms:
-
"SampleEstimator" construct a sample moment estimator "UnbiasedSampleEstimator" construct an unbiased sample moment estimator - Sample moment expressions can be considered a random variable constructed from independent, identically distributed random variables. The expected value can be found by converting from its sample moment expression to a moment expression.
- The expectation for a given sample moment expression can be computed using the forms:
-
"Moment" express in terms of formal moments "CentralMoment" express in terms of formal central moments "FactorialMoment" express in terms of formal factorial moments "Cumulant" express in terms of formal cumulants - MomentConvert[expr,form1,form2,…] first converts to form1, then to form2, etc.
Examples
open all close allBasic Examples (2)
Express the cumulant in terms of raw moments:
Express the multivariate cumulant in terms of central moments:
Find an unbiased sample estimator for the second cumulant, i.e. second k-statistics:
Convert the estimator to the basis of power symmetric polynomials:
Compute expectation of the estimator in terms of raw moments:
Scope (4)
Express a multivariate cumulant in terms of raw moments:
Find an unbiased sample estimator for a product of univariate central moments, also known as polyache:
Find the sampling distribution estimator expectation of an augmented symmetric polynomial:
Convert the augmented symmetric polynomial to the basis of power symmetric polynomials:
Evaluate at a sample of size 3:
Compare to direct evaluation of the augmented symmetric polynomial:
Generalizations & Extensions (2)
Applications (21)
Converting Formal Moments (2)
Analysis of Estimators (6)
Compute a sample estimator of the variance:
Compute the bias of the estimator as the mean with respect to the sampling population distribution, assuming a sample of size ![]() :
:
Illustrate the computation by evaluating the estimator on a symbolic sample of size 5:
Now compute its expectation assuming ![]() are independent random variates from normal distribution:
are independent random variates from normal distribution:
Compare with the result obtained above:
Compute the expected variance of a sample estimator of the variance:
Compute the variance as the second central moment of the estimator:
In the large sample size limit, the variance of the estimator tends to zero in agreement with the law of large numbers:
Perform 1000 simulations using standard normal samples of size 30:
Compare the sample mean and variance to their expected values:
Compute covariance between the sample mean and sample variance estimators:
Compute sampling population covariance as a mixed central moment:
The expected covariance vanishes on normal samples:
Find a sample estimator of the off-diagonal covariance matrix element of two-dimensional data:
Find its bias and its variance:
Compute the bias and the variance of the estimator for binormal samples:
Estimate the sample size needed for the variance of the estimator on standard binormal samples with ![]() not to exceed 0.001:
not to exceed 0.001:
The sample estimator of the standard deviation is computed as the square root of the sample variance:
Such an estimator is biased and underestimates the population standard deviation:
The analysis of the standard deviation estimator is carried out by replacing the nonlinear function with its truncated Taylor series about the bias of its argument:
Find the expectation of the approximated estimator:
Compute its numerical value for a standard normal sample of size ![]() :
:
Find the variance of the estimator for normal samples:
Derive finite-sample Jarque–Bera statistics ![]() :
:
Find the mean and variance of sample skewness estimator ![]() on size
on size ![]() normal samples:
normal samples:
Compute the mean and variance of sample kurtosis estimator ![]() on size
on size ![]() normal samples:
normal samples:
Unbiased Raw Moment Estimators (2)
Unbiased Factorial Moment Estimators (1)
Unbiased Central Moment Estimators (3)
Write the h-statistics in terms of power symmetric polynomials:
Compare it with the sample estimator of the second central moment ![]() :
:
Find the sampling population expectation of these estimators for sample size ![]() :
:
Compute the third h-statistics in terms of power symmetric polynomials:
Compare it with the sample estimator of central moment ![]() :
:
Find the sampling population expectation of these estimators for sample size ![]() :
:
Find multivariate h-statistics for ![]() :
:
Evaluate the estimator on a sample from a binormal distribution:
Unbiased Cumulant Estimators (2)
Compound Estimators (3)
Find the unbiased estimator of the second power of mean:
Evaluate it on a symbolic sample:
Find the sample population expectation:
Compute the unbiased estimator of the product of cumulants, also known as polykay:
Express it in terms of power symmetric polynomials:
Find the unbiased estimator of the product of multivariate central moments, also known as polyache:
Cumulants of k-Statistics (1)
Cumulants of k-statistics are polynomials in sampling population expectations of certain monomials of k-statistics. They are built using umbral calculus, starting with expression of the multivariate cumulant in terms of raw moments:
Each multivariate moment is understood as the sampling population expectation of the monomial in k-statistics. For instance, raw moment ![]() stands for the product of expectation of
stands for the product of expectation of ![]() . Find the resulting unbiased estimator for
. Find the resulting unbiased estimator for ![]() and
and ![]() :
:
Define a procedure for computation of cumulants of k-statistics:
This implies that the sample mean and sample variance of a normal sample are independent:
Cumulants of k-statistics were tabulated because they were thought to give more concise expressions, and were used for computation of moments of estimators. Compute the cumulant of second k-statistics:
Compute the cumulant of the product of k-statistics:
Expressions for higher-order cumulants of k-statistics quickly become big:
Properties & Relations (5)
The binomial theorem defines relations between formal moments and formal central moments:
Express formal factorial moments in terms of formal moments using Stirling numbers:
Polynomial in moments rewritten in terms of central moments may still involve the mean ![]() :
:
The sample estimator of factorial moment is unbiased:
Compute cumulants through series expansion of logarithm of moment-generating function:
Possible Issues (2)
Conversion between forms of symmetric polynomials treats formal moments as constants:
Expressions involving AugmentedSymmetricPolynomial and PowerSymmetricPolynomial are converted:
MomentConvert requires input to be polynomial in formal and/or sample moments:
Related Guides
History
Text
Wolfram Research (2010), MomentConvert, Wolfram Language function, https://reference.wolfram.com/language/ref/MomentConvert.html.
CMS
Wolfram Language. 2010. "MomentConvert." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MomentConvert.html.
APA
Wolfram Language. (2010). MomentConvert. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MomentConvert.html
BibTeX
@misc{reference.wolfram_2025_momentconvert, author="Wolfram Research", title="{MomentConvert}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/MomentConvert.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_momentconvert, organization={Wolfram Research}, title={MomentConvert}, year={2010}, url={https://reference.wolfram.com/language/ref/MomentConvert.html}, note=[Accessed: 25-January-2026]}