Map

Map[f,expr] or f/@expr

applies f to each element on the first level in expr.

Map[f,expr,levelspec]

applies f to parts of expr specified by levelspec.

Map[f]

represents an operator form of Map that can be applied to an expression.

Details and Options

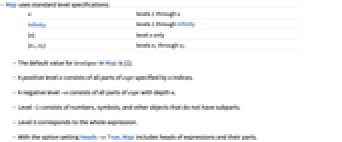
  • Map uses standard level specifications:
  • nlevels 1 through n
    Infinitylevels 1 through Infinity
    {n}level n only
    {n1,n2}levels n1 through n2
  • The default value for levelspec in Map is {1}.
  • A positive level n consists of all parts of expr specified by n indices.
  • A negative level -n consists of all parts of expr with depth n.
  • Level –1 consists of numbers, symbols, and other objects that do not have subparts.
  • Level 0 corresponds to the whole expression.
  • With the option setting Heads->True, Map includes heads of expressions and their parts.
  • Map always effectively constructs a complete new expression and then evaluates it.
  • If expr is an Association object, Map[f,expr] applies f to the values in the association.
  • If expr is a SparseArray object, Map[f,expr] applies f to the values or subarrays that appear in expr.
  • Map[f][expr] is equivalent to Map[f,expr].

Examples

open allclose all

Basic Examples  (8)

In[1]:=
Click for copyable input
Out[1]=

Alternative input form:

In[1]:=
Click for copyable input
Out[1]=

Use explicit pure functions:

In[1]:=
Click for copyable input
Out[1]=
In[2]:=
Click for copyable input
Out[2]=

Map at top level:

In[1]:=
Click for copyable input
Out[1]=

Map at level 2:

In[2]:=
Click for copyable input
Out[2]=

Map at levels 1 and 2:

In[3]:=
Click for copyable input
Out[3]=

Use a map operator:

In[1]:=
Click for copyable input
Out[1]=

Map a function over values in Association:

In[1]:=
Click for copyable input
Out[1]=

Map at the second level of a nested Association:

In[1]:=
Click for copyable input
Out[1]=

Map at several levels in an Association:

In[1]:=
Click for copyable input
Out[1]=

Scope  (6)

Generalizations & Extensions  (4)

Options  (1)

Applications  (4)

Properties & Relations  (5)

Possible Issues  (1)

Neat Examples  (1)

See Also

Apply  Scan  MapAll  MapAt  MapIndexed  MapThread  AssociationMap  KeyMap  KeyValueMap  Level  Operate  Through  Thread  ParallelMap  ImageApply

Tutorials

Introduced in 1988
(1.0)
| Updated in 2014
(10.0)