MapIndexed

MapIndexed[f,expr]

applies f to the elements of expr, giving the part specification of each element as a second argument to f.

MapIndexed[f,expr,levelspec]

applies f to all parts of expr on levels specified by levelspec.

MapIndexed[f]

represents an operator form of MapIndexed that can be applied to an expression.

Details and Options

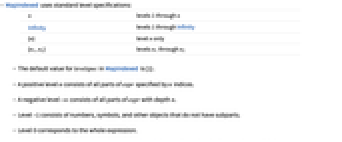
  • MapIndexed uses standard level specifications:
  • nlevels 1 through n
    Infinitylevels 1 through Infinity
    {n}level n only
    {n1,n2}levels n1 through n2
  • The default value for levelspec in MapIndexed is {1}.
  • A positive level n consists of all parts of expr specified by n indices.
  • A negative level -n consists of all parts of expr with depth n.
  • Level –1 consists of numbers, symbols, and other objects that do not have subparts.
  • Level 0 corresponds to the whole expression.
  • With the option setting Heads->True, MapIndexed also applies to heads of expressions and their parts.
  • MapIndexed always effectively constructs a complete new expression and then evaluates it.
  • MapIndexed works on SparseArray objects, effectively by applying Normal to them.
  • MapIndexed works on Association objects, giving part specifications in the form Key[k].
  • MapIndexed[f][expr] is equivalent to MapIndexed[f,expr].
  • Parallelize[MapIndexed[f,expr]] computes MapIndexed[f,expr] in parallel on all subkernels. »

Examples

open allclose all

Basic Examples  (6)

#2 gives the indices of each part:

Map over an association:

Map over nested associations:

Use the operator form of MapIndexed:

Scope  (6)

Level Specifications  (6)

Map at level 1 (default):

Map down to level 2:

Map at level 2:

Map down to level 3:

Map onto all elements of an expression:

Map only onto the "leaves" of the expression:

Negative levels:

Different heads at each level:

Map on levels 0 through 1; the head has index {}:

Generalizations & Extensions  (3)

MapIndexed can be used on expressions with any head:

The function can be mapped onto the heads as well:

MapIndexed works on sparse arrays:

Options  (2)

Heads  (2)

By default, the function is not mapped onto the heads:

Map onto the heads at all levels:

Applications  (5)

Label parts by position:

Use tooltips to show part numbers of subexpressions:

Convert a list to a polynomial:

Rotate lists based on position:

Obtain a list of all parts in an expression:

Properties & Relations  (3)

Using only the first argument is equivalent to using Map:

The result of MapIndexed on an association is closely related to the result of KeyValueMap:

Use a combination of Values and Part to obtain the same result:

Compute MapIndexed in parallel:

Wolfram Research (1991), MapIndexed, Wolfram Language function, https://reference.wolfram.com/language/ref/MapIndexed.html (updated 2014).

Text

Wolfram Research (1991), MapIndexed, Wolfram Language function, https://reference.wolfram.com/language/ref/MapIndexed.html (updated 2014).

CMS

Wolfram Language. 1991. "MapIndexed." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/MapIndexed.html.

APA

Wolfram Language. (1991). MapIndexed. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MapIndexed.html

BibTeX

@misc{reference.wolfram_2024_mapindexed, author="Wolfram Research", title="{MapIndexed}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MapIndexed.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mapindexed, organization={Wolfram Research}, title={MapIndexed}, year={2014}, url={https://reference.wolfram.com/language/ref/MapIndexed.html}, note=[Accessed: 21-November-2024 ]}