LinearSolveFunction[dimensions,data]
represents a function for providing solutions to a matrix equation.


LinearSolveFunction
LinearSolveFunction[dimensions,data]
represents a function for providing solutions to a matrix equation.
Details
- LinearSolveFunction[…] is generated by LinearSolve[m].
- LinearSolveFunction works like Function.
- LinearSolveFunction[…][b] finds the solution to the matrix equation
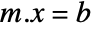 for the specific vector or matrix
for the specific vector or matrix 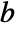 .
. - dimensions specifies the dimensions of the matrix m from which the LinearSolveFunction was constructed.
Examples
open all close allBasic Examples (1)
Scope (3)
Generalizations & Extensions (1)
Applications (2)
Find the eigenvector associated with the smallest eigenvalue:
Approximate value of the eigenvalue:
Expressions for a finite difference approximation to the Laplacian in 2 dimensions:
A matrix approximating the Laplacian operator:
A linear solve function for the matrix:
An approximate solution for the Poisson equation ![]() on the unit rectangle:
on the unit rectangle:
An approximate solution for the Poisson equation ![]() on the unit rectangle:
on the unit rectangle:
Properties & Relations (2)
A LinearSolveFunction is effectively like a matrix inverse. A large sparse matrix:
Time to compute and memory used by the linear solve function:
Time to compute and memory used by the inverse matrix:
Comparison of f and the inverse matrix for a random vector b:
Create a LinearSolveFunction for a simple matrix:
Compute the inverse matrix from f:
Compute the inverse matrix using Inverse:
Related Guides
History
Introduced in 2003 (5.0)
Text
Wolfram Research (2003), LinearSolveFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/LinearSolveFunction.html.
CMS
Wolfram Language. 2003. "LinearSolveFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LinearSolveFunction.html.
APA
Wolfram Language. (2003). LinearSolveFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LinearSolveFunction.html
BibTeX
@misc{reference.wolfram_2025_linearsolvefunction, author="Wolfram Research", title="{LinearSolveFunction}", year="2003", howpublished="\url{https://reference.wolfram.com/language/ref/LinearSolveFunction.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_linearsolvefunction, organization={Wolfram Research}, title={LinearSolveFunction}, year={2003}, url={https://reference.wolfram.com/language/ref/LinearSolveFunction.html}, note=[Accessed: 25-January-2026]}