Lists
Lists
In doing calculations, it is often convenient to collect together several objects, and treat them as a single entity. Lists give you a way to make collections of objects in the Wolfram Language. As you will see later, lists are very important and general structures in the Wolfram Language.
A list such as {3,5,1} is a collection of three objects. But in many ways, you can treat the whole list as a single object. You can, for example, do arithmetic on the whole list at once, or assign the whole list to be the value of a variable.
This takes differences between corresponding elements in the two lists. The lists must be the same length:
You can apply any of the mathematical functions in "Some Mathematical Functions" to whole lists:
We first encountered lists in "Making Lists of Objects" as a way of collecting numbers together. Here, we shall see many different ways to use lists. You will find that lists are some of the most flexible and powerful objects in the Wolfram Language. You will see that lists in the Wolfram Language represent generalizations of several standard concepts in mathematics and computer science.
At a basic level, what a Wolfram Language list essentially does is to provide a way for you to collect together several expressions of any kind.
The mathematical functions that are built into the Wolfram Language are mostly set up to be "listable" so that they act separately on each element of a list. This is, however, not true of all functions in the Wolfram Language. Unless you set it up specially, a new function f that you introduce will treat lists just as single objects. "Applying Functions to Parts of Expressions" and "Structural Operations" will describe how you can use Map and Thread to apply a function like this separately to each element in a list.
You can use lists as tables of values. You can generate the tables, for example, by evaluating an expression for a sequence of different parameter values.
Table uses exactly the same iterator notation as the functions Sum and Product, which are discussed in "Sums and Products":
You can perform other operations on the lists you get from Table:
TableForm displays lists in a "tabular" format. Notice that both words in the name TableForm begin with capital letters:
All the examples so far have been of tables obtained by varying a single parameter. You can also make tables that involve several parameters. These multidimensional tables are specified using the standard Wolfram Language iterator notation, discussed in "Sums and Products".
The table in this example is a list of lists. The elements of the outer list correspond to successive values of 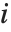 . The elements of each inner list correspond to successive values of
. The elements of each inner list correspond to successive values of 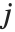 , with
, with 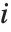 fixed.
fixed.
Sometimes you may want to generate a table by evaluating a particular expression many times, without incrementing any variables.
This gives a list of four pairs of numbers sampled from {1,2,3,4}. Table reevaluates RandomSample[{1,2,3,4},2] for each element in the list, so that you get four different samples:
You can use Table to generate arrays with any number of dimensions.
| Table[f,{imax}] | give a list of imax values of f |
| Table[f,{i,imax}] | give a list of the values of f as i runs from 1 to imax |
| Table[f,{i,imin,imax}] | give a list of values with i running from imin to imax |
| Table[f,{i,imin,imax,di}] | use steps of di |
| Table[f,{i,imin,imax},{j,jmin,jmax},…] | generate a multidimensional table |
| Table[f,{i,{i1,i2,…}] | give a list of the values of f as i successively takes the values i1, i2, … |
| TableForm[list] | display a list in tabular form |
You can use the operations discussed in "Manipulating Elements of Lists" to extract elements of the table.
| t[[i]] or Part[t,i] | give the i th sublist in t (also input as t〚i〛) |
| t[[i;;j]] or Part[t,i;;j] | give a list of the parts i through j |
| t[[{i1,i2,…}]] or Part[t,{i1,i2,…}] | give a list of the i1 th, i2 th, … parts of t |
| t[[i,j,…]] or Part[t,i,j,…] | give the part of t corresponding to t[[i]][[j]]… |
As mentioned in "Manipulating Elements of Lists", you can think of lists in the Wolfram Language as being analogous to "arrays". Lists of lists are then like two‐dimensional arrays. When you lay them out in a tabular form, the two indices of each element are like its 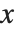 and
and 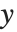 coordinates.
coordinates.
Many of the most powerful list manipulation operations in the Wolfram Language treat whole lists as single objects. Sometimes, however, you need to pick out or set individual elements in a list.
You can refer to an element of a Wolfram Language list by giving its "index". The elements are numbered in order, starting at 1.
| {a,b,c} | a list |
| Part[list,i] or list[[i]] | the i th element of list (the first element is list[[1]]) |
| Part[list,{i,j,…}] or list[[{i,j,…}]] | a list of the i th, j th, … elements of list |
| Part[list,i;;j] | a list of the i th through j th elements of list |
By assigning a variable to be a list, you can use Wolfram Language lists much like "arrays" in other computer languages. Thus, for example, you can reset an element of a list by assigning a value to v[[i]].
| Part[v,i] or v[[i]] | extract the i th element of a list |
| Part[v,i]=value or v[[i]]=value | reset the i th element of a list |
Vectors and matrices in the Wolfram Language are simply represented by lists and by lists of lists, respectively.
Because of the way the Wolfram Language uses lists to represent vectors and matrices, you never have to distinguish between "row" and "column" vectors.
| Table[f,{i,n}] | build a length‐n vector by evaluating f with i=1,2,…,n |
| Array[a,n] | build a length‐n vector of the form {a[1],a[2],…} |
| Range[n] | create the list {1,2,3,…,n} |
| Range[n1,n2] | create the list {n1,n1+1,…,n2} |
| Range[n1,n2,dn] | create the list {n1,n1+dn,…,n2} |
| list[[i]] or Part[list,i] | give the i th element in the vector list |
| Length[list] | give the number of elements in list |
| c v | multiply a vector by a scalar |
| a.b | dot product of two vectors |
| Cross[a,b] |
cross product of two vectors (also input as
a×b
)
|
| Norm[v] | Euclidean norm of a vector |
| Table[f,{i,m},{j,n}] | build an m×n matrix by evaluating f with i ranging from 1 to m and j ranging from 1 to n |
| Array[a,{m,n}] | build an m×n matrix with i,j th element a[i,j] |
| IdentityMatrix[n] | generate an n×n identity matrix |
| DiagonalMatrix[list] | generate a square matrix with the elements in list on the main diagonal |
| list[[i]] or Part[list,i] | give the i th row in the matrix list |
| list[[All,j]] or Part[list,All,j] | give the j th column in the matrix list |
| list[[i,j]] or Part[list,i,j] | give the i,j th element in the matrix list |
| Dimensions[list] | give the dimensions of a matrix represented by list |
| Column[list] | display the elements of list in a column |
| MatrixForm[list] | display list in matrix form |
This gives a vector with symbolic elements. You can use this in deriving general formulas that are valid with any choice of vector components:
This gives a 3×2 matrix with symbolic elements. "Building Lists from Functions" discusses how you can produce other kinds of elements with Array:
| c m | multiply a matrix by a scalar |
| a.b | dot product of two matrices |
| Inverse[m] | matrix inverse |
| MatrixPower[m,n] | n th power of a matrix |
| Det[m] | determinant |
| Tr[m] | trace |
| Transpose[m] | transpose |
| Eigenvalues[m] | eigenvalues |
| Eigenvectors[m] | eigenvectors |
Eigenvalues gives the eigenvalues of the matrix:
"Linear Algebra in Wolfram Language" discusses many other matrix operations that are built into the Wolfram Language.
| First[list] | the first element in list |
| Last[list] | the last element |
| Part[list,n] or list[[n]] | the n th element |
| Part[list,-n] or list[[-n]] | the n th element from the end |
| Part[list,m;;n] | elements m through n |
| Part[list,{n1,n2,…}] or list[[{n1,n2,…}]] | |
the list of elements at positions n1, n2, … | |
| Take[list,n] | the first n elements in list |
| Take[list,-n] | the last n elements |
| Take[list,{m,n}] | elements m through n (inclusive) |
| Rest[list] | list with its first element dropped |
| Drop[list,n] | list with its first n elements dropped |
| Most[list] | list with its last element dropped |
| Drop[list,-n] | list with its last n elements dropped |
| Drop[list,{m,n}] | list with elements m through n dropped |
"Manipulating Expressions like Lists" shows how all the functions here can be generalized to work not only on lists, but on any Wolfram Language expressions.
The functions here allow you to pick out pieces that occur at particular positions in lists. "Finding Expressions That Match a Pattern" shows how you can use functions like Select and Cases to pick out elements of lists based not on their positions, but instead on their properties.
| Position[list,form] | the positions at which form occurs in list |
| Count[list,form] | the number of times form appears as an element of list |
| MemberQ[list,form] | test whether form is an element of list |
| FreeQ[list,form] | test whether form occurs nowhere in list |
"Getting Pieces of Lists" discusses how to extract pieces of lists based on their positions or indices. The Wolfram System also has functions that search and test for elements of lists, based on the values of those elements.
As discussed in "Finding Expressions That Match a Pattern", the functions Count and Position, as well as MemberQ and FreeQ, can be used not only to search for particular list elements, but also to search for classes of elements which match specific "patterns".
| Prepend[list,element] | add element at the beginning of list |
| Append[list,element] | add element at the end of list |
| Insert[list,element,i] | insert element at position i in list |
| Insert[list,element,-i] | insert at position i counting from the end of list |
| Riffle[list,element] | interleave element between the entries of list |
| Delete[list,i] | delete the element at position i in list |
| ReplacePart[list,i->new] | replace the element at position i in list with new |
| ReplacePart[list,{i,j}->new] | replace list[[i,j]] with new |
Functions like ReplacePart take explicit lists and give you new lists. Sometimes, however, you may want to modify a list "in place", without explicitly generating a new list.
| m[[i,j]]=new | replace the (i,j) th element of a matrix |
| m[[i]]=new | replace the i th row |
| m[[All,i]]=new | replace the i th column |
| Join[list1,list2,…] | concatenate lists together |
| Union[list1,list2,…] |
combine lists, removing repeated elements and sorting the result
|
| Riffle[list1,list2] | interleave elements of list1 and list2 |
Join concatenates any number of lists together:
Union combines lists, keeping only distinct elements:
Riffle combines lists by interleaving their elements:
The Wolfram Language usually keeps the elements of a list in exactly the order you originally entered them. If you want to treat a Wolfram Language list like a mathematical set, however, you may want to ignore the order of elements in the list.
| Union[list1,list2,…] | give a list of the distinct elements in the listi |
| Intersection[list1,list2,…] | give a list of the elements that are common to all the listi |
| Complement[universal,list1,…] | give a list of the elements that are in universal, but not in any of the listi |
| Subsets[list] | give a list of all subsets of the elements in list |
| DeleteDuplicates[list] | delete all duplicates from list |
Union gives the elements that occur in any of the lists:
Intersection gives only elements that occur in all the lists:
Complement gives elements that occur in the first list, but not in any of the others:
DeleteDuplicates deletes all duplicate elements from the list:
| Sort[list] | sort the elements of list into a standard order |
| Union[list] |
sort elements, removing any duplicates
|
| Reverse[list] | reverse the order of elements in list |
| RotateLeft[list,n] | rotate the elements of list n places to the left |
| RotateRight[list,n] | rotate n places to the right |
This sorts the elements of a list into a standard order. In simple cases like this, the order is alphabetical or numerical:
You can rotate to the right by giving a negative displacement, or by using RotateRight:
| PadLeft[list,len,x] | pad list on the left with x to make it length len |
| PadRight[list,len,x] | pad list on the right |
| Partition[list,n] | partition list into n‐element pieces |
| Partition[list,n,d] | use offset d for successive pieces |
| Split[list] | split list into pieces consisting of runs of identical elements |
| SplitBy[list,f] | split list into runs of elements with identical values when f is applied |
| Gather[list] | gather the elements of list into sublists of identical elements |
| GatherBy[list,f] | gather the elements of list into sublists with identical values when f is applied |
| Tuples[list,n] | generate all possible n‐tuples of elements from list |
| Tuples[{list1,list2,…}] | generate all tuples whose i th element is from listi |
| Sort[list] | sort the elements of list into order |
| Ordering[list] | the positions in list of the elements in Sort[list] |
| Ordering[list,n] | the first n elements of Ordering[list] |
| Ordering[list,-n] | the last n elements of Ordering[list] |
| Permutations[list] | all possible orderings of list |
| Min[list] | the smallest element in list |
| Max[list] | the largest element in list |
This gives the positions of the elements of t, from the position of the smallest to that of the largest:
This is the same as Sort[t]:
You will encounter nested lists if you use matrices or generate multidimensional arrays and tables. The Wolfram Language provides many functions for handling such lists.
| Flatten[list] | flatten out all levels in list |
| Flatten[list,n] | flatten out the top n levels in list |
| Partition[list,{n1,n2,…}] | partition into blocks of size n1×n2×… |
| Transpose[list] | interchange the top two levels of lists |
| RotateLeft[list,{n1,n2,…}] | rotate successive levels by ni places |
| PadLeft[list,{n1,n2,…}] | pad successive levels to be length ni |
There are many other operations you can perform on nested lists. More operations are discussed in "Manipulating Lists".