FourierSeries`
FourierSeries`
FourierCoefficient
As of Version 7.0, FourierCoefficient is part of the built-in Wolfram Language kernel.
FourierCoefficient[expr,t,n]
gives the n![]() coefficient in the Fourier exponential series expansion of expr, where expr is a periodic function of t with period 1.
coefficient in the Fourier exponential series expansion of expr, where expr is a periodic function of t with period 1.
Details and Options
- To use FourierCoefficient, you first need to load the Fourier Series Package using Needs["FourierSeries`"].
- The n
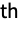 coefficient in the Fourier exponential series expansion of expr is by default defined to be Integrate[expr 2πnt,{t,-
coefficient in the Fourier exponential series expansion of expr is by default defined to be Integrate[expr 2πnt,{t,-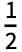 ,
,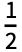 }].
}]. - If n is numeric, it should be an explicit integer.
- Different choices for the definition of the Fourier exponential series expansion can be specified using the option FourierParameters.
- With the setting FourierParameters->{a,b}, expr is assumed to have a period of
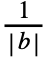 , and the n
, and the n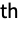 coefficient computed by FourierCoefficient is
coefficient computed by FourierCoefficient is 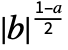 Integrate[expr 2 πbnt,{t,-
Integrate[expr 2 πbnt,{t,-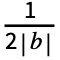 ,
,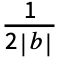 }].
}]. - In addition to the option FourierParameters, FourierCoefficient can also accept the options available to Integrate. These options are passed directly to Integrate.
Examples
Wolfram Research (2008), FourierCoefficient, Wolfram Language function, https://reference.wolfram.com/language/FourierSeries/ref/FourierCoefficient.html.
Text
Wolfram Research (2008), FourierCoefficient, Wolfram Language function, https://reference.wolfram.com/language/FourierSeries/ref/FourierCoefficient.html.
CMS
Wolfram Language. 2008. "FourierCoefficient." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/FourierSeries/ref/FourierCoefficient.html.
APA
Wolfram Language. (2008). FourierCoefficient. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FourierSeries/ref/FourierCoefficient.html