FourierSeries

As of Version 7.0, FourierSeries is part of the built-in Wolfram System kernel.

FourierSeries[expr,t,n]

gives the order n Fourier exponential series expansion of expr, where expr is a periodic function of t with period 1.

Details and Options

To use FourierSeries, you first need to load the Fourier Series Package using Needs["FourierSeries`"].
The order n Fourier exponential series expansion of expr is by default defined to be 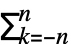F_k^2πkt, where F_k is given by Integrate[expr ^2πkt,{t,-,}].
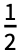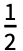Different choices for the period of expr can be specified using the option FourierParameters.
With the setting FourierParameters->{a,b}, expr is assumed to have a period of 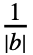, and the order n Fourier exponential series expansion computed by FourierSeries is 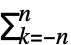F_k^2πkt, where F_k is given by bIntegrate[expr ^2πbkt,{t,-,}].
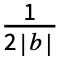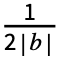In addition to the option FourierParameters, FourierSeries can also accept the options available to Integrate. These options are passed directly to Integrate.