Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Wolfram Language & System Documentation Center

FourierSinCoefficient

FourierSeries`

FourierSeries`

FourierSinCoefficient

バージョン7.0の時点で，FourierSinCoefficientは組込みのWolfram言語カーネルの一部となっている．

FourierSinCoefficient[expr,t,n]

expr のフーリエ正弦級数展開の第 n 係数を与える．ここで expr は周期1の t の周期関数である．

詳細とオプション

FourierSinCoefficientを使うためには，まずフーリエ級数パッケージをロードしなくてはならない．それにはNeeds["FourierSeries`"]を実行する必要がある．
expr のフーリエ正弦級数展開の第 n 係数は，デフォルトで2Integrate[expr Sin[2π n t],{t,-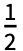,}]となっている．
n が数値の場合，明示的に整数でなければならない．
異なるフーリエ正弦級数展開の定義は，オプションFourierParametersを使って指定することができる．
FourierParameters->{a,b}という設定では，expr は周期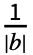を持つものと想定され，FourierSinCoefficientで計算される第 n 係数は2 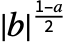Integrate[expr Sin[2π b n t],{t,-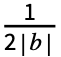,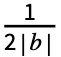}]である．
FourierSinCoefficientはオプションFourierParametersの他，Integrateで使用できるオプションを取ることもできる．これらのオプションは直接Integrateに渡される．

例題

例 (1)

フーリエ正弦級数の係数を計算するために異なる定義を使う：

数値近似からの解と比較する：

Top