WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

FourierSeries`

FourierSeries`

InverseDTFourierTransform

バージョン7.0の時点で，InverseDTFourierTransformはInverseFourierSequenceTransformという名前に変更され，組込みのWolfram言語カーネルの一部となっている．

InverseDTFourierTransform[expr,ω,n]

expr の離散時間逆フーリエ変換を返す．ここで expr は周期1の ω の周期関数である．

詳細とオプション

InverseDTFourierTransformを使うためには，まずフーリエ級数パッケージをロードしなくてはならない．それにはNeeds["FourierSeries`"]を実行する必要がある．
expr の離散時間逆フーリエ変換は，デフォルトでIntegrate[expr ^-2πnω,{ω,-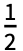,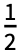}]となっている．
n が数値の場合，明示的な整数でなければならない．
異なる離散時間逆フーリエ変換の定義は，オプションFourierParametersを使って指定することができる．
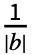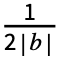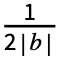FourierParameters->{a,b}という設定では，expr は周期を持つと想定され，InverseDTFourierTransformで計算される離散時間逆フーリエ変換は Integrate[expr ^-2πω,{ω,-,}]である．
InverseDTFourierTransformはオプションFourierParametersの他，Integrateで使用できるオプションを取ることができる．これらのオプションは直接Integrateに渡される．

例題

例 (1)

指定された離散時間フーリエ変換の数列を見付ける：

数値近似からの解と比較する：

トップへ