MultivariateStatistics`
MultivariateStatistics`
SpearmanRankCorrelation
As of Version 9.0, SpearmanRankCorrelation has been renamed to SpearmanRho and is part of the built-in Wolfram Language kernel.
SpearmanRankCorrelation[xlist,ylist]
gives Spearman's rank correlation coefficient 
for the real‐valued vectors xlist and ylist.
更多信息和选项
- To use SpearmanRankCorrelation, you first need to load the Multivariate Statistics Package using Needs["MultivariateStatistics`"].
- Spearman's rank correlation coefficient is a measure of association based on the rank differences between two lists.
- Spearman's
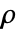is given by 
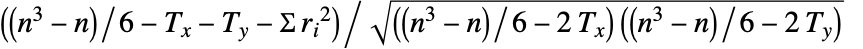, where n=Length[xlist], 
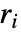is the rank difference between 
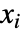and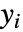 
, 
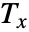is the correction term for ties in xlist, and 
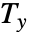is the correction term for ties in ylist. - The arguments xlist and ylist can be any real‐valued vectors of equal length.
范例
Wolfram Research (2007)，SpearmanRankCorrelation，Wolfram 语言函数，https://reference.wolfram.com/language/MultivariateStatistics/ref/SpearmanRankCorrelation.html.
文本
Wolfram Research (2007)，SpearmanRankCorrelation，Wolfram 语言函数，https://reference.wolfram.com/language/MultivariateStatistics/ref/SpearmanRankCorrelation.html.
CMS
Wolfram 语言. 2007. "SpearmanRankCorrelation." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/MultivariateStatistics/ref/SpearmanRankCorrelation.html.
APA
Wolfram 语言. (2007). SpearmanRankCorrelation. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/MultivariateStatistics/ref/SpearmanRankCorrelation.html 年