PrimalityProving`
PrimalityProving`

PrimeQCertificate

PrimeQCertificate[n]

n が素数である，あるいは n が合成数であるという証明書を返す．

詳細とオプション

  • PrimeQCertificateを使うためには，まず素数証明パッケージをロードしなくてはならない．それにはNeeds["PrimalityProving`"]を実行する必要がある．
  • PrimeQCertificateでは，素数性に対してプラットおよびAtkin–Morainの証明書を使用する．
  • 合成性の証明書は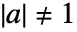で{a,n-1,n}，あるいは{a,2,n}という3つの整数のリストである．
  • 素数 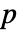は常に 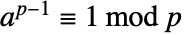を満足する．証明書{a,n-1,n}は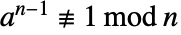， であることを示すことにより n が合成数であることを証明するために使うことができる．
  • 素数 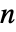について，平方が 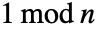となるような任意の数 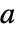は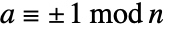， を満足しなければならない．証明書{a,2,n}は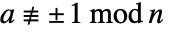， であり 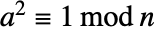であることを示すことにより n が合成数であることを証明するために使うことができる．
  • 素数証明書は，1つ以上の 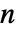より小さい数が素数であれば 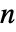も素数であるということを証明する証明書の回帰リストで構成される．
  • PrimeQCertificateにはProvablePrimeQと同じオプションがある．

例題

例  (2)

1093が素数であることを証明するために使うことのできる証明書：

ProvablePrimeQをオプション"Certificate"->Trueで使うことで同じ証明書が得られる：

1093×3511が合成数であることを証明するために使うことのできる証明書：

出力は，1093×3511が合成数であり， が素数のときに というフェルマ(Fermat)の素数の小定理に反することを示す3つの整数のリストである．