Details and Options


Examples
Basic Examples
Scope
Options
Certificate
PrimeQMessages
Properties & Relations
Possible Issues
See Also
Tech Notes
Related Guides
PrimalityProving`
PrimalityProving`
ProvablePrimeQ
Details and Options
- To use ProvablePrimeQ, you first need to load the Primality Proving Package using Needs["PrimalityProving`"].
- When ProvablePrimeQ[n] returns True, then n is prime based on the Pratt certificate of primality or the Atkin–Morain certificate of primality.
- ProvablePrimeQ should not be used as a replacement for PrimeQ, as PrimeQ is several orders of magnitude faster. Instead, use ProvablePrimeQ to certify the results of PrimeQ when needed.
- The following options can be given:
-
"SmallPrime" 1050 lower bound for using the Atkin–Morain test "Certificate" False whether to print a certificate "PollardPTest" Automatic whether to use the Pollard 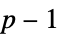 method
method"PollardRhoTest" Automatic whether to use the Pollard 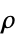 method
method"TrialDivisionLimit" Automatic number of primes to use in trial division "PrimeQMessages" False whether progress is to be monitored
Examples
open all close allBasic Examples (1)
PrimeQ indicates that 1093 is prime:
ProvablePrimeQ gives the same result, but it has generated a certificate:
Scope (2)
Options (2)
Properties & Relations (1)
If ProvablePrimeQ has returned a result, use PrimeQCertificate to print the certificate:
With "Certificate"->True, ProvablePrimeQ repeats the Atkin–Morain primality test: