WOLFRAM

Wolfram Language & System Documentation Center

BesselFilterModel[n]

designs a lowpass Bessel filter of order n and cutoff frequency 1.

BesselFilterModel[{n,ωc}]

uses the cutoff frequency ωc.

BesselFilterModel[{n,ωc},var]

expresses the model in terms of the variable var.

Details
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Applications  
Properties & Relations  
See Also
Related Guides
History
Cite this Page

BesselFilterModel

BesselFilterModel[n]

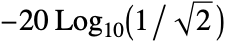designs a lowpass Bessel filter of order n and cutoff frequency 1.

BesselFilterModel[{n,ωc}]

uses the cutoff frequency ωc.

BesselFilterModel[{n,ωc},var]

expresses the model in terms of the variable var.

Details

Examples

open all close all

Basic Examples  (2)

A third-order Bessel filter model with cutoff frequency at :

Bode plot of the modeled filter:

A sixth-order lowpass Bessel filter with cutoff frequency at :

Magnitude response of the filter showing the ideal filter characteristics:

Scope  (1)

A symbolic representation of an order-2 lowpass filter:

A second-order Bessel filter model with cutoff frequency at :

Applications  (1)

Create a lowpass Bessel filter:

Filter out high-frequency noise from a sinusoidal signal:

Create a highpass Bessel filter from the lowpass prototype:

Filter out low-frequency sinusoid from the input:

Properties & Relations  (4)

Show the denominator of the transfer function as a Bessel polynomial:

Find the poles of a Bessel filter by solving for the roots of the denominator:

Extract poles using TransferFunctionPoles:

Implement a lowpass digital Bessel filter:

Convert a lowpass filter to high pass:

Wolfram Research (2012), BesselFilterModel, Wolfram Language function, https://reference.wolfram.com/language/ref/BesselFilterModel.html.

Text

Wolfram Research (2012), BesselFilterModel, Wolfram Language function, https://reference.wolfram.com/language/ref/BesselFilterModel.html.

CMS

Wolfram Language. 2012. "BesselFilterModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BesselFilterModel.html.

APA

Wolfram Language. (2012). BesselFilterModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BesselFilterModel.html

BibTeX

@misc{reference.wolfram_2025_besselfiltermodel, author="Wolfram Research", title="{BesselFilterModel}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/BesselFilterModel.html}", note=[Accessed: 09-August-2025]}

BibLaTeX

@online{reference.wolfram_2025_besselfiltermodel, organization={Wolfram Research}, title={BesselFilterModel}, year={2012}, url={https://reference.wolfram.com/language/ref/BesselFilterModel.html}, note=[Accessed: 09-August-2025]}