gives the n![]() Catalan number
Catalan number ![]() .
.


CatalanNumber
gives the n![]() Catalan number
Catalan number ![]() .
.
Details
- CatalanNumber[n] is generically defined as
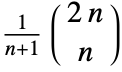 .
. - Catalan numbers are integers for integer arguments, and appear in various tree enumeration problems.
- CatalanNumber can be used with Interval and CenteredInterval objects: »
Examples
open all close allScope (9)
Evaluate for half-integer arguments:
Evaluate for complex arguments:
Plot the Catalan number as a function of its index:
Compute sums involving CatalanNumber:
CatalanNumber threads element-wise over lists:
CatalanNumber can be used with Interval and CenteredInterval objects:
TraditionalForm typesetting:
Applications (3)
Compute the number of different ways to parenthesize an expression:
Distribute over lists in CirclePlus:
Use the pattern matcher to repeatedly split the list into two parts in all possible ways:
The number of ways to parenthesize the expression a⊕b⊕c⊕d:
The Catalan numbers CatalanNumber[n] can be characterized as the unique set of numbers such that two Hankel determinants are both equal to one. Verify for the first few cases:
Verify an expression for the Catalan numbers in terms of double factorials:
Properties & Relations (6)
The generating function for Catalan numbers:
Catalan numbers can be represented as a difference of binomial coefficients:
Catalan numbers can be represented in terms of the generalized Bell polynomial:
CatalanNumber can be represented as a DifferenceRoot:
FindSequenceFunction can recognize the CatalanNumber sequence:
The exponential generating function for CatalanNumber:
Possible Issues (1)
Neat Examples (2)
The only odd Catalan numbers are those of the form CatalanNumber[2k-1]:
Determinants of Hankel matrices made out of sums of Catalan numbers:
Compare with an expression in terms of the Fibonacci numbers:
See Also
Function Repository: FussCatalanNumber DyckWords DelannoyD CatalanUnrank CatalanRank
Tech Notes
Related Guides
Text
Wolfram Research (2007), CatalanNumber, Wolfram Language function, https://reference.wolfram.com/language/ref/CatalanNumber.html (updated 2014).
CMS
Wolfram Language. 2007. "CatalanNumber." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/CatalanNumber.html.
APA
Wolfram Language. (2007). CatalanNumber. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CatalanNumber.html
BibTeX
@misc{reference.wolfram_2025_catalannumber, author="Wolfram Research", title="{CatalanNumber}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/CatalanNumber.html}", note=[Accessed: 09-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_catalannumber, organization={Wolfram Research}, title={CatalanNumber}, year={2014}, url={https://reference.wolfram.com/language/ref/CatalanNumber.html}, note=[Accessed: 09-December-2025]}