CatalanNumber

CatalanNumber[n]

n 番目のカタラン数 TemplateBox[{n}, CatalanNumber]を与える．

詳細

  • CatalanNumber[n]は，一般的に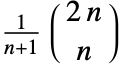と定義される．
  • カタラン数は整数引数のための整数であり，さまざまな木の列挙問題に現れる．
  • CatalanNumberはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例  (1)

最初の10個のカタラン数：

スコープ  (9)

大きい引数について評価する：

半整数引数について評価する：

数値的に評価する：

複素引数について評価する：

カタラン数をその下付き文字の関数としてプロットされる：

CatalanNumberを含む総和を計算する：

CatalanNumberはリストに対して要素単位で適用される：

CatalanNumberはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる：

TraditionalFormによる表示：

アプリケーション  (3)

式をカッコでくくるさまざまな方法の数を計算する：

CirclePlusでリスト上に分布させる：

パターンマッチングを使って，可能なすべての方法で，繰返しリストを2分割していく：

式a⊕b⊕c⊕dをカッコでくくる方法の数：

検証する：

カタラン数CatalanNumber[n]は，2つのハンケル行列式がどちらも1と等しくなる数の一意的な集合として特徴付けられる．最初の数例について検証する：

カタラン数についての式を二重階乗によって確認する：

特性と関係  (6)

カタラン数の母関数：

カタラン数は二項係数の差として表すことができる：

型乱数は一般化されたベル多項式によって表すことができる：

CatalanNumberはDifferenceRootとして表すことができる：

FindSequenceFunctionはCatalanNumber数列を認識する：

CatalanNumberの指数母関数：

考えられる問題  (1)

カタラン数r TemplateBox[{{-, 1}}, CatalanNumber]は，慣例により，その二項表現によって定義される：

値は解析関数の極限値とは異なる：

おもしろい例題  (2)

奇数のカタラン数はCatalanNumber[2k-1]という形式のカタラン数だけである：

カタラン数の和からなるハンケル行列の行列式：

フィボナッチ数による式と比較する：

Wolfram Research (2007), CatalanNumber, Wolfram言語関数， https://reference.wolfram.com/language/ref/CatalanNumber.html （2014年に更新）.

テキスト

Wolfram Research (2007), CatalanNumber, Wolfram言語関数， https://reference.wolfram.com/language/ref/CatalanNumber.html （2014年に更新）.

CMS

Wolfram Language. 2007. "CatalanNumber." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/CatalanNumber.html.

APA

Wolfram Language. (2007). CatalanNumber. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CatalanNumber.html

BibTeX

@misc{reference.wolfram_2024_catalannumber, author="Wolfram Research", title="{CatalanNumber}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/CatalanNumber.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_catalannumber, organization={Wolfram Research}, title={CatalanNumber}, year={2014}, url={https://reference.wolfram.com/language/ref/CatalanNumber.html}, note=[Accessed: 21-November-2024 ]}