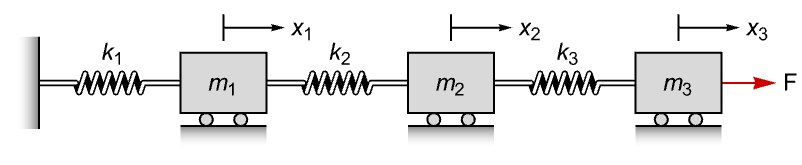
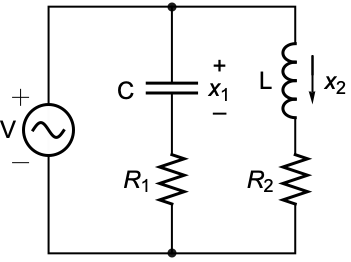
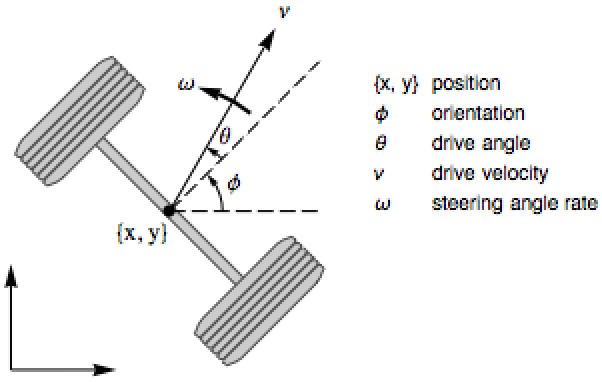
ControllableModelQ[sys]
ControllableModelQ[{sys,sub}]
部分系 sub が可制御であればTrueを返す.


ControllableModelQ
ControllableModelQ[sys]
ControllableModelQ[{sys,sub}]
部分系 sub が可制御であればTrueを返す.
詳細とオプション

- ControllableModelQは到達可能モデルとしても知られている.
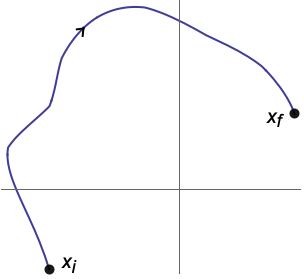
- 任意の初期状態
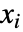 と最終状態
と最終状態 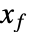 について有限時間内に状態を
について有限時間内に状態を 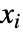 から
から 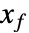 に向ける制御入力が存在する場合,その状態空間モデルは可制御であると言われる.
に向ける制御入力が存在する場合,その状態空間モデルは可制御であると言われる. - 系 sys は標準またはディスクリプタのStateSpaceModelあるいはAffineStateSpaceModelでよい.
- 次の部分系 sub を指定することができる. » »
-
All 系全体 "Fast" 速い部分系 "Slow" 遅い部分系 {λ1,…} 固有モード 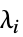 の部分系
の部分系 - "Fast"および"Slow"の部分系は,KroneckerModelDecompositionで説明されているように,主にディスクリプタ状態空間モデルに適用される.
- 固有モード λiについてはJordanModelDecompositionに説明がある.
- ControllableModelQには次の設定のMethodオプションが使える.
-
Automatic 適切な検定を自動的に選択する "Distribution" 可制御性分布の階数を使う "Gramian" 可制御性グラミアンの階数または正定性を使う "Matrix" 可制御性行列の階数を使う "PBH" Popov–Belevitch–Hautus階数検定を使う
例題
すべて開く すべて閉じるスコープ (6)
可制御性は遅いモードの可制御性と速いモードの可制御性の両方について等価である(C−可制御性):
このことは,ジョルダン形(第3状態に影響を与える方法がない)にも見られる:
AffineStateSpaceModelの可制御性の検定を行う:
オプション (7)
Method (7)
デフォルトで,可制御性行列は厳密系と記号系の両方に使われる:
ControllabilityMatrixが最大階数であればその系は可制御である:
ControllabilityGramianが最大階数であれば,その系は可制御である:
可制御性グラミアンにとって,このことは,それ自身が正定であることと同義である:
他の数値系にはPopov–Belevitch–Hautus階数検定が用いられる:
![]() がすべての
がすべての ![]() について最大階数であるので,この系は可制御である:
について最大階数であるので,この系は可制御である:
線形系では,可制御性行列と可制御性分布に基づいた検定は等しい:
入力線形系の行列検定は,線形化された系に対して"Matrix"メソッドを使う:
アプリケーション (5)
特性と関係 (7)
![]() の場合は,第1状態を直接制御することはできない.しかし,第2状態から間接的に制御することは可能である:
の場合は,第1状態を直接制御することはできない.しかし,第2状態から間接的に制御することは可能である:
![]() の場合は,第2状態は,直接制御することも第1状態から間接的に制御することもできない:
の場合は,第2状態は,直接制御することも第1状態から間接的に制御することもできない:
JordanModelDecompositionを使って,上記の正準状態空間表現を計算する:
ディスクリプタ系については,KroneckerModelDecompositionは対角形の一般化である:
StateSpaceModelのディスクリプタ行列が最大階数である場合には,速い部分系は存在しない:
したがって,系の完全な可制御性は,遅い部分系から評価することができる:
可制御性は非特異StateSpaceTransformのもとでは不変である:
StateFeedbackGainsを使って状態フィードバックを計算する:
可制御性はその出力が可制御であることを意味しない(OutputControllableModelQ):
関連するガイド
-
▪
- 状態空間モデルの解析 ▪
- 非線形制御系
テキスト
Wolfram Research (2010), ControllableModelQ, Wolfram言語関数, https://reference.wolfram.com/language/ref/ControllableModelQ.html (2014年に更新).
CMS
Wolfram Language. 2010. "ControllableModelQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ControllableModelQ.html.
APA
Wolfram Language. (2010). ControllableModelQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ControllableModelQ.html
BibTeX
@misc{reference.wolfram_2025_controllablemodelq, author="Wolfram Research", title="{ControllableModelQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ControllableModelQ.html}", note=[Accessed: 07-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_controllablemodelq, organization={Wolfram Research}, title={ControllableModelQ}, year={2014}, url={https://reference.wolfram.com/language/ref/ControllableModelQ.html}, note=[Accessed: 07-March-2026]}