JordanModelDecomposition

JordanModelDecomposition[ssm]

yields the Jordan decomposition of the state-space model ssm.

Details

  • The result is a list {p,jc}, where p is a similarity matrix, and jc is the Jordan canonical form of ssm.
  • The state-space model ssm can be given as StateSpaceModel[{a,b,c,d}], where a, b, c, and d represent the state, input, output, and transmission matrices in either a continuous-time or a discrete-time system:
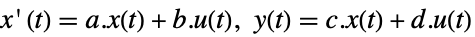
  • continuous-time system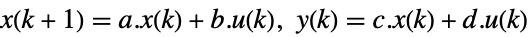
    discrete-time system
  • The transformation 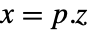, where 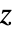is the new state vector, and 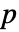is a similarity matrix that spans the linearly independent eigenvectors of 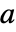, transforms the system into the Jordan canonical form:
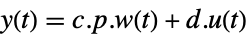
  • w'(t)=TemplateBox[{p}, Inverse].a.p.w(t)+TemplateBox[{p}, Inverse].b.u(t), continuous-time system
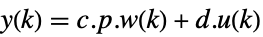    w(k+1)=TemplateBox[{p}, Inverse].a.p.w(k)+TemplateBox[{p}, Inverse].b.u(k),.discrete-time system
  • The new state matrix TemplateBox[{p}, Inverse].a.p is the Jordan canonical form of the old state matrix .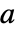

Examples

open allclose all

Basic Examples  (1)

Compute the Jordan decomposition of a state-space model:

Scope  (4)

The Jordan decomposition of a second-order system:

The Jordan decomposition of a discrete-time system:

A transformation that gives the complex poles in second-order blocks:

Repeated poles appear in Jordan blocks:

Applications  (2)

A system is controllable if and only if the Jordan blocks of have distinct eigenvalues, and the row of corresponding to the last row of each Jordan block is not zero:

A system is observable if and only if the Jordan blocks of have distinct eigenvalues, and the column of corresponding to the first row of each Jordan block is not zero:

Properties & Relations  (3)

In the Jordan canonical form, the eigenvalues are along the diagonal of the state matrix:

The Jordan canonical form is related to the original system via the similarity transform:

The Jordan canonical form of a state-space model is the similarity transformation associated with the Jordan decomposition of its state matrix:

Possible Issues  (1)

JordanModelDecomposition does not support descriptor systems:

Use KroneckerModelDecomposition to separate the modes of the system:

Wolfram Research (2010), JordanModelDecomposition, Wolfram Language function, https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

Text

Wolfram Research (2010), JordanModelDecomposition, Wolfram Language function, https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

CMS

Wolfram Language. 2010. "JordanModelDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

APA

Wolfram Language. (2010). JordanModelDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JordanModelDecomposition.html

BibTeX

@misc{reference.wolfram_2025_jordanmodeldecomposition, author="Wolfram Research", title="{JordanModelDecomposition}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/JordanModelDecomposition.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_jordanmodeldecomposition, organization={Wolfram Research}, title={JordanModelDecomposition}, year={2010}, url={https://reference.wolfram.com/language/ref/JordanModelDecomposition.html}, note=[Accessed: 21-February-2025 ]}