ControllableDecomposition[sys]
yields the controllable subsystem of the state-space model sys.
ControllableDecomposition[sys,{z1,…}]
specifies the new state variables zi.


ControllableDecomposition
ControllableDecomposition[sys]
yields the controllable subsystem of the state-space model sys.
ControllableDecomposition[sys,{z1,…}]
specifies the new state variables zi.
Details and Options
- ControllableDecomposition gives {p,csys}, where p is the transformation and csys is the controllable subsystem.
- The system sys can be a standard or descriptor StateSpaceModel or AffineStateSpaceModel.
- The controllable subsystem is given by StateSpaceTransform[sys,p].
- ControllableDecomposition accepts a Method option. The following settings can be specified:
-
Automatic automatically choose the method "Matrix" use the controllability matrix "Distribution" use the controllability distribution
Examples
open all close allScope (4)
Applications (7)
Linear Systems (4)
Construct the Kalman controllable decomposition:
ControllableDecomposition picks out the controllable subsystem only:
Kalman controllable decomposition puts the controllable subsystem first and keeps the rest:
Compute the dimension of the controllable subspace:
The controllable subspace is the range of p, i.e. the column dimension:
Find the controllable subspace for the system below and explain the possible state trajectories that can occur in the system:
The system is uncontrollable, so only a subspace is controllable:
The range of the transformation matrix p gives the controllable subspace:
Trajectories can be controlled in this subspace:
But you cannot control the drift between parallel copies of the controllable subspace:
Design a controller for a system that is not completely controllable, by building a controller for the controllable subsystem:
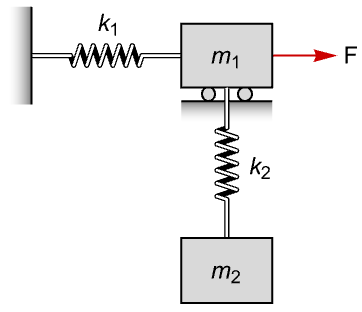
Since a force applied only on the first mass ![]() , the second mass
, the second mass ![]() is not controllable:
is not controllable:
Design a controller using the controllable subsystem:
Use the transformation to obtain the controller for the original system:
The simulation shows controlled as well as oscillatory modes in the closed-loop system:
Affine Systems (3)
Construct the triangular controllability decomposition:
ControllableDecomposition picks out the controllable subsystem only:
Triangular controllability decomposition puts the controllable subsystem first and keeps the rest:
Compute the dimension of the controllable subspace:
The dimension can be obtained from the inverse transformation ![]() :
:
The controllable decomposition gives the reachable subspace and subsystem. This can be used to visualize the motion of the system from one subspace to another:
The generic reachable subspace:
A specific reachable subspace:
Select several initial points on this surface:
All these initial points end up at exactly the same final surface because that motion is not controllable:
A 3D plot shows the motion from the initial surface to the final one:
Properties & Relations (2)
The transformation matrix p selects the controllable subsystem using StateSpaceTransform:
For affine systems, the transformation rules select the controllable subsystem:
Related Guides
Text
Wolfram Research (2010), ControllableDecomposition, Wolfram Language function, https://reference.wolfram.com/language/ref/ControllableDecomposition.html (updated 2014).
CMS
Wolfram Language. 2010. "ControllableDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ControllableDecomposition.html.
APA
Wolfram Language. (2010). ControllableDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ControllableDecomposition.html
BibTeX
@misc{reference.wolfram_2025_controllabledecomposition, author="Wolfram Research", title="{ControllableDecomposition}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ControllableDecomposition.html}", note=[Accessed: 12-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_controllabledecomposition, organization={Wolfram Research}, title={ControllableDecomposition}, year={2014}, url={https://reference.wolfram.com/language/ref/ControllableDecomposition.html}, note=[Accessed: 12-January-2026]}