DiscreteLQRegulatorGains[sspec,wts,τ]
重み wts の費用関数を最小にする連続時間系指定 sspec のサンプリング周期 τ による離散時間状態フィードバックゲインを与える.
DiscreteLQRegulatorGains[…,"prop"]
特性"prop"の値を与える.


DiscreteLQRegulatorGains
DiscreteLQRegulatorGains[sspec,wts,τ]
重み wts の費用関数を最小にする連続時間系指定 sspec のサンプリング周期 τ による離散時間状態フィードバックゲインを与える.
DiscreteLQRegulatorGains[…,"prop"]
特性"prop"の値を与える.
詳細とオプション








- DiscreteLQRegulatorGainsは,離散線形二次調整器,離散線形二次調整器相当,あるいは離散線形二次エミュレーテッド調整器としても知られている.
- DiscreteLQRegulatorGainsは,一般に,調整コントローラあるいは追跡コントローラのデジタル実装の計算に使われる.
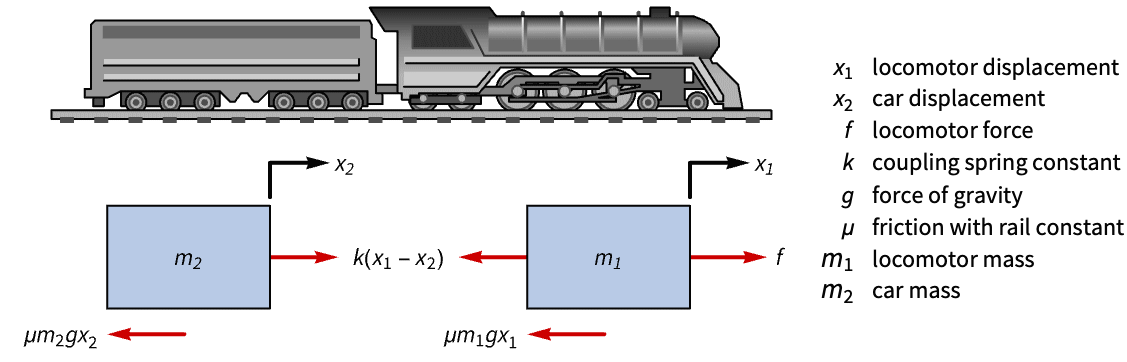
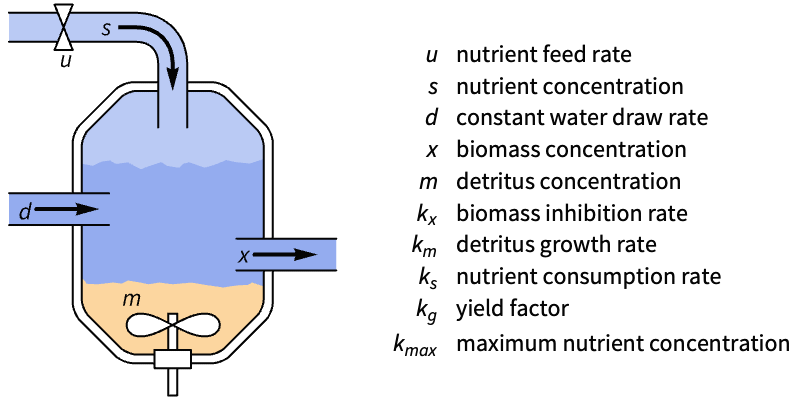
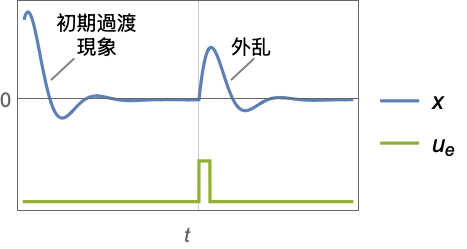
- 調整コントローラは,系を乱そうとする外乱
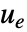 があっても系を平衡状態に保とうとする.典型的な例として,直立した倒立振子や水平飛行中の航空機等が挙げられる.
があっても系を平衡状態に保とうとする.典型的な例として,直立した倒立振子や水平飛行中の航空機等が挙げられる. - 調整コントローラは
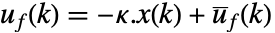 の形の制御規則で与えられる.ただし,
の形の制御規則で与えられる.ただし, は計算されたゲイン行列である.
は計算されたゲイン行列である. - 連続時間費用関数は
 で与えられる.
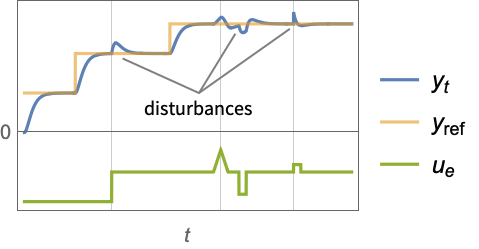
で与えられる. - 追跡コントローラは,それを妨害する外乱
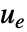 があっても参照信号を追跡しようとする.典型的な例として,自動車のクルーズコントロールシステムやロボットの経路追跡が挙げられる.
があっても参照信号を追跡しようとする.典型的な例として,自動車のクルーズコントロールシステムやロボットの経路追跡が挙げられる. - 追跡コントローラは
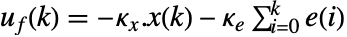 の形の制御規則で与えられる.ただし,
の形の制御規則で与えられる.ただし,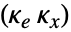 は系 sys と
は系 sys と  のダイナミクスを含む拡張系のための計算されたゲイン行列である.
のダイナミクスを含む拡張系のための計算されたゲイン行列である. - 近似離散時間系:
- 連続時間費用関数は
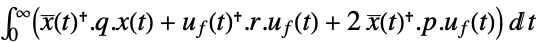 で与えられる.ただし,
で与えられる.ただし,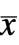 は拡張状態である.
は拡張状態である. - 拡張状態の数は
 で与えられる.ただし,
で与えられる.ただし,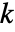 は sys のSystemsModelOrderで,
は sys のSystemsModelOrderで,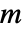 は yref の次数で,
は yref の次数で, は信号 yrefの数で与えられる.
は信号 yrefの数で与えられる. - 重み行列の選択は,結果としてパフォーマンスと制御努力のトレードオフとなり,優れた設計に反復的に到達する.初期値は成分が
![TemplateBox[{{1, /, z}, i, 2}, Subsuperscript] TemplateBox[{{1, /, z}, i, 2}, Subsuperscript]](Files/DiscreteLQRegulatorGains.ja/21.png) の対角行列でよい.ただし,ziは対応する xiまたは uiの許容可能な最大絶対値である.
の対角行列でよい.ただし,ziは対応する xiまたは uiの許容可能な最大絶対値である. - DiscreteLQRegulatorGainsは,連続時間費用関数に相当する離散時間の近似を使って離散時間コントローラを計算する.
- 離散時間近似費用関数は以下の項を持つ
![sum_(k=0)^infty(x^^(k).phi.x^^(k)+TemplateBox[{{{u, _, f}, (, k, )}}, ConjugateTranspose].rho.u_f(k)+2 TemplateBox[{{{x, ^, ^}, (, k, )}}, ConjugateTranspose].psi.u_f(k)) sum_(k=0)^infty(x^^(k).phi.x^^(k)+TemplateBox[{{{u, _, f}, (, k, )}}, ConjugateTranspose].rho.u_f(k)+2 TemplateBox[{{{x, ^, ^}, (, k, )}}, ConjugateTranspose].psi.u_f(k))](Files/DiscreteLQRegulatorGains.ja/22.png) である.
である. -
状態重み行列 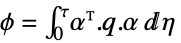
入力重み行列 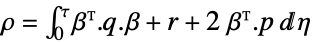
クロスカップリング重み行列 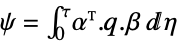
状態ベクトル 調整には 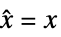 ,追跡には
,追跡には 
- 重み wts は次の形でよい.
-
{q,r} クロスカップリングがない費用関数 {q,r,p} クロスカップリング行列 p がある費用関数 - 系の指定 sspec は,系 sys と指定 uf,yt,yrefである.
- 系 sys はStateSpaceModel[{a,b,c,d}]として与えることができる.ただし,a, b, c, d は,連続時間系
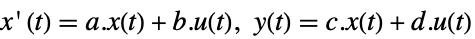 の,状態,入力,出力,フィードスルー行列である.
の,状態,入力,出力,フィードスルー行列である. - 離散時間設計モデル dsys は次の項を持つ0次のホールド近似
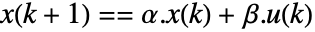 である.
である. -
状態行列 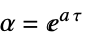
入力行列 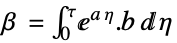
- 系の指定 sspec は以下の形でよい.
-
StateSpaceModel[…] 線形制御入力と線形状態 AffineStateSpaceModel[…] 線形制御入力と非線形状態 NonlinearStateSpaceModel[…] 非線形制御入力と非線形状態 SystemModel[…] 一般的な系のモデル <|…|> Associationとして与えられる詳細な系の指定 - 系の指定の詳細は次のキーを持つことができる.
-
"InputModel" sys モデルの任意のもの "FeedbackInputs" All フィードバック入力 uf "TrackedOutputs" None 追跡された出力 yt "TrackedSignal" Automatic yrefのダイナミクス - フィードバック入力は次の形でよい.
-
{num1,…,numn} StateSpaceModel, AffineStateSpaceModel,NonlinearStateSpaceModelで使われる番号付き入力 numi {name1,…,namen} SystemModelで使われる名前付き入力 namei All すべての入力を使う - AffineStateSpaceModel,NonlinearStateSpaceModel,SystemModelのような非線形系については,系は保存された動作点の周りで線形化される.
- DiscreteLQRegulatorGains[…,"Data"]は cd["prop"]の形で追加的な特性の抽出に使えるSystemsModelControllerDataオブジェクト cd を返す.
- DiscreteLQRegulatorGains[…,"prop"]を使って cd["prop"]の値を直接与えることができる.
- 次は,特性"prop"の可能な値である.
-
"BlockDiagram" csys のブロック図 "ClosedLoopSystem" サンプルデータ閉ループ系 csys {"ClosedLoopSystem",cspec} csys の形式についての詳細制御 "Design" コントローラ設計のタイプ "DesignModel" 設計に使用されるモデル "DiscreteTimeBlockDiagram" dcsys のブロック図 "DiscreteTimeClosedLoopPoles" "DiscreteTimeClosedLoopSystem"の極 "DiscreteTimeClosedLoopSystem" dcsys {"DiscreteTimeClosedLoopSystem",cspec} 離散時間閉ループ系を統合するかどうか "DiscreteTimeControllerModel" dcm "DiscreteTimeDesignModel" 近似された離散時間モデル dsys "DiscreteTimeFeedbackGainsModel" dgm または {dgm1,dgm2} "DiscreteTimeOpenLoopPoles" dsys の極 "DiscreteTimeWeights" 近似された費用の重み ϕ, ρ, π "FeedbackGains" ゲイン行列 κ またはそれに相当するもの "FeedbackInputs" フィードバックに使われる sys の入力 uf "InputCount" sys の入力 u の数 "InputModel" 入力モデル sys "OpenLoopPoles" "DesignModel"の極 "OutputCount" sys の出力 y の数 "SamplingPeriod" サンプリング period τ "StateCount" sys の状態 x の数 "TrackedOutputs" 追跡された sys の出力 ytの数 - 次は, cspec の可能なキーである.
-
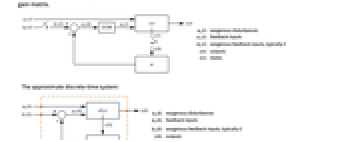
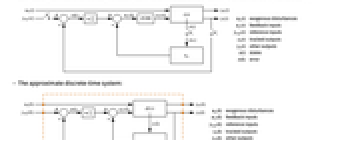
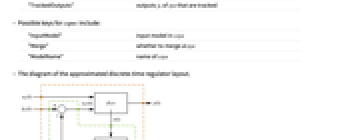
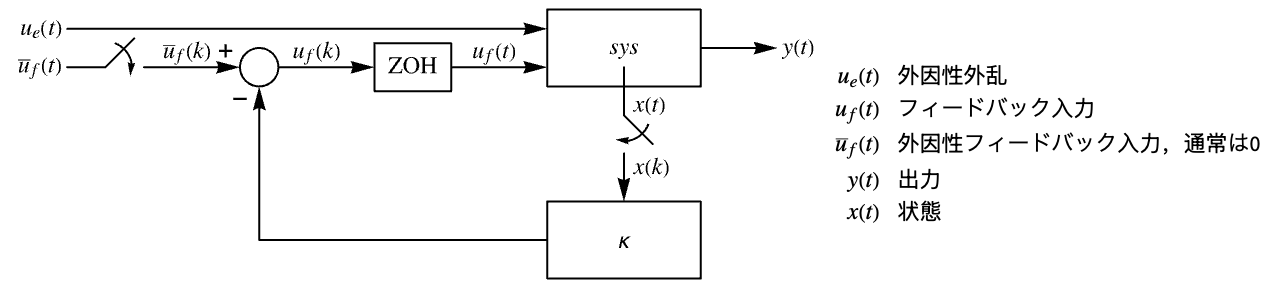
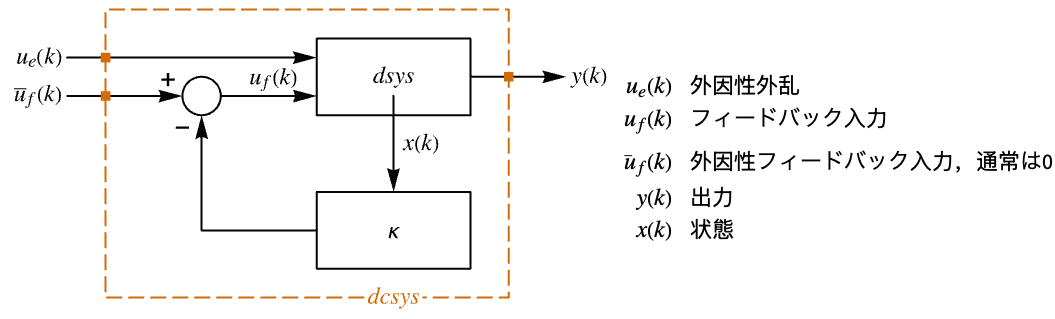
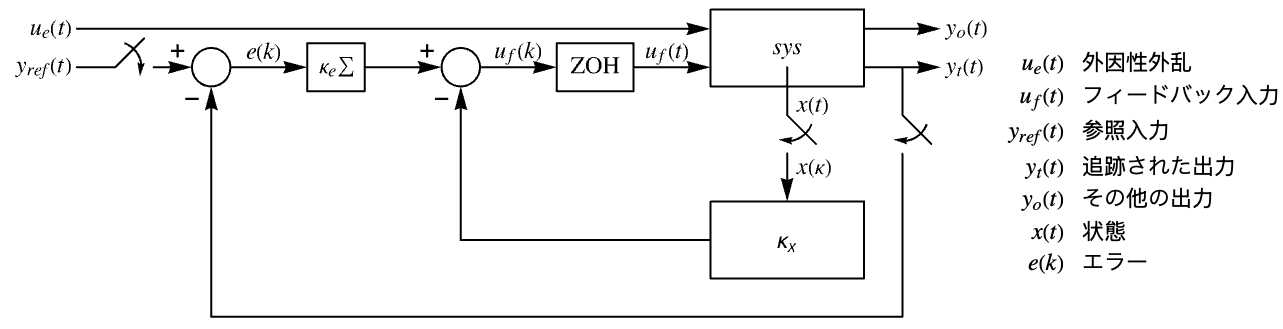
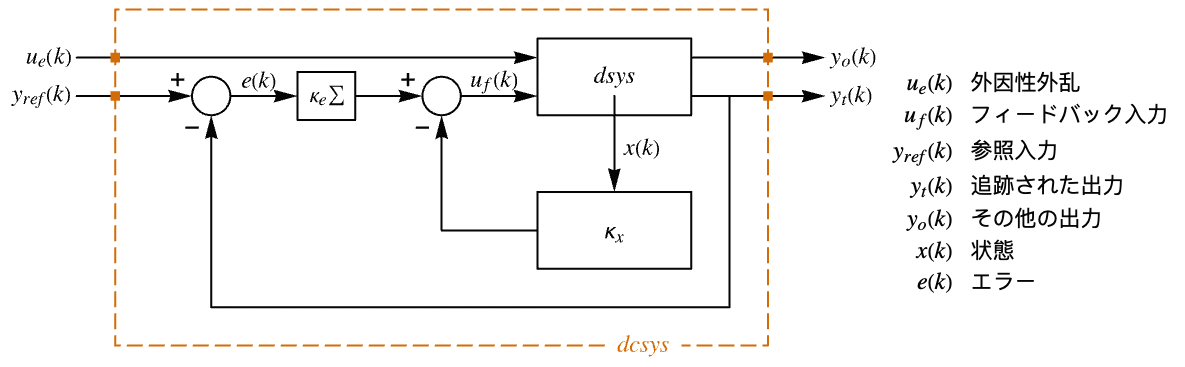
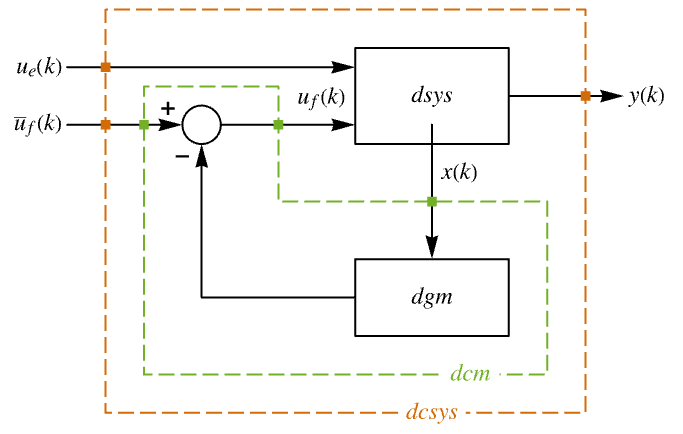
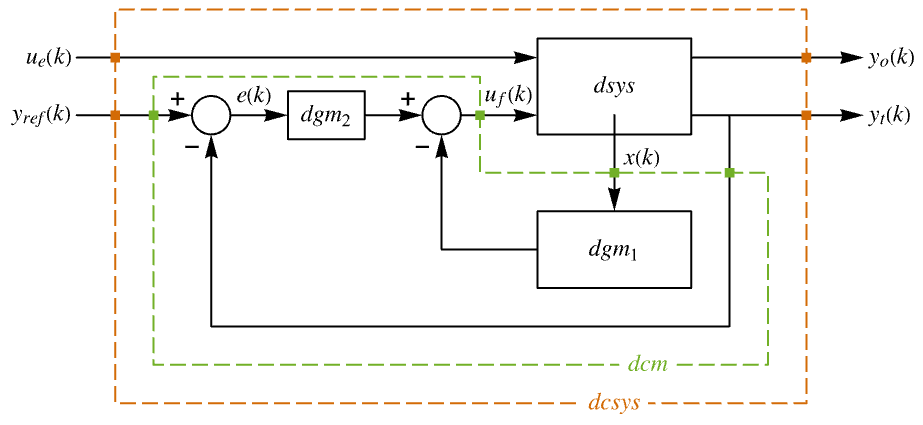
"InputModel" csys の入力モデル "Merge" csys を統合するどうか "ModelName" csys の名前 - 次は,近似離散時間調整器のレイアウトの線図である.
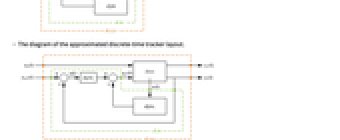
- 次は,近似離散時間追跡器のレイアウトの線図である.
例題
すべて開く すべて閉じる例 (4)
スコープ (30)
工場のモデル (5)
特性 (14)
DiscreteLQRegulatorGainsは,デフォルトで,離散時間フィードバックゲインを返す:
アプリケーション (12)
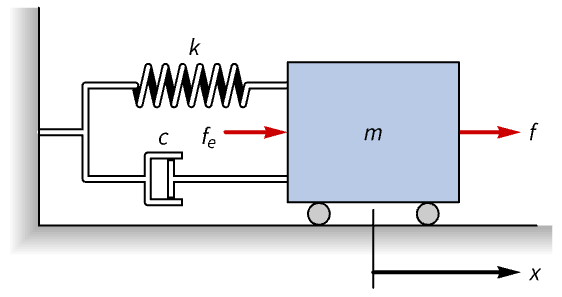
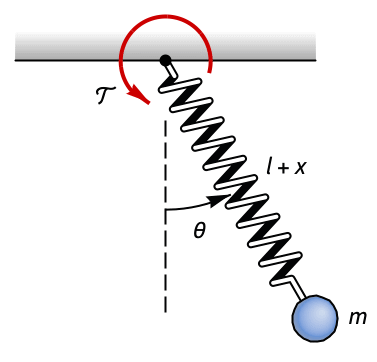
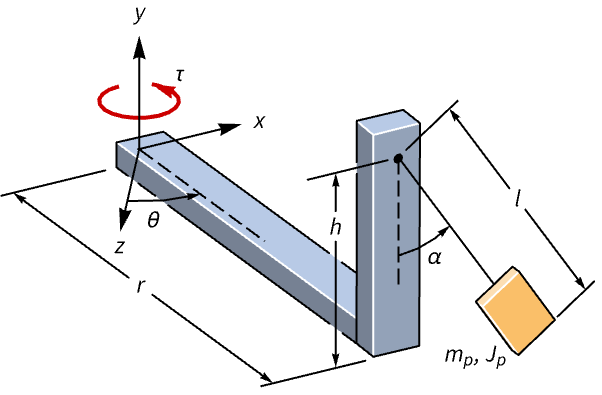
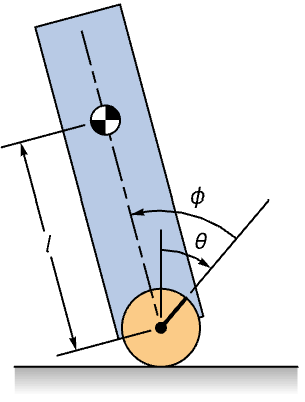
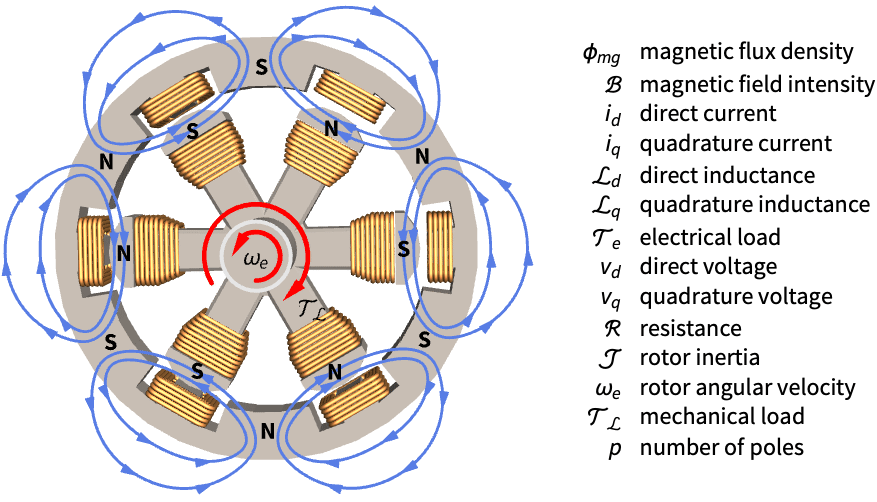
機械系 (5)
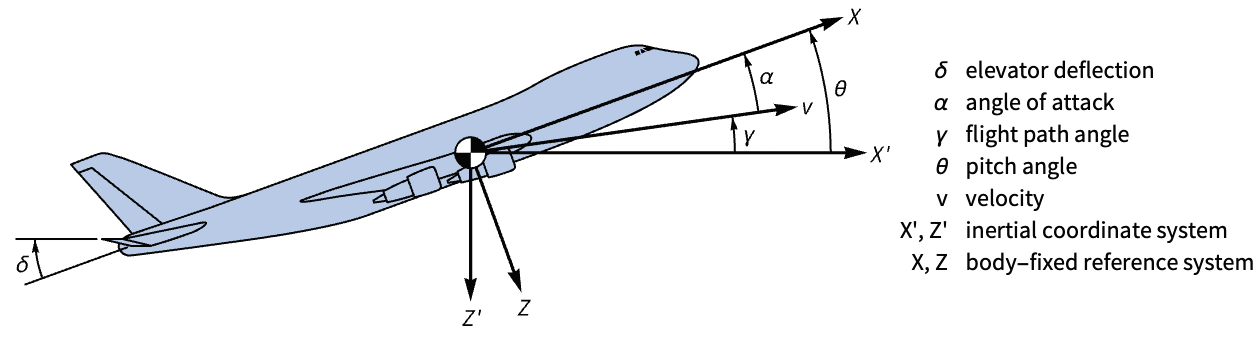
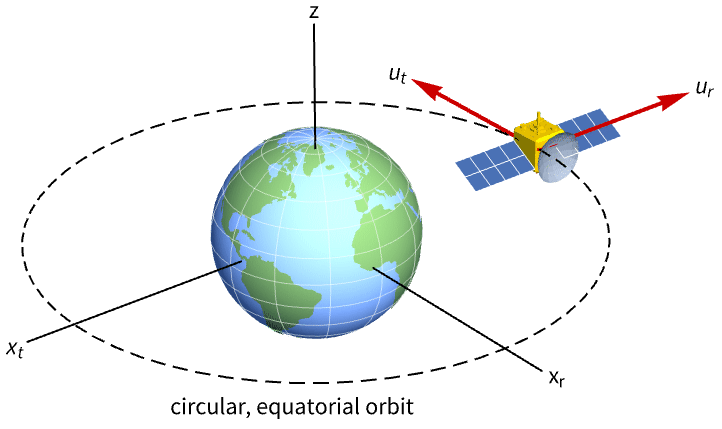
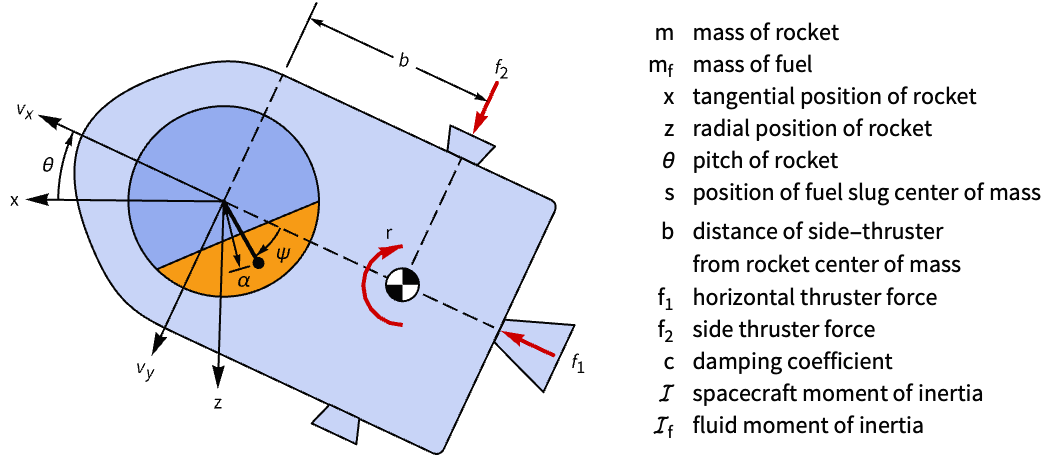
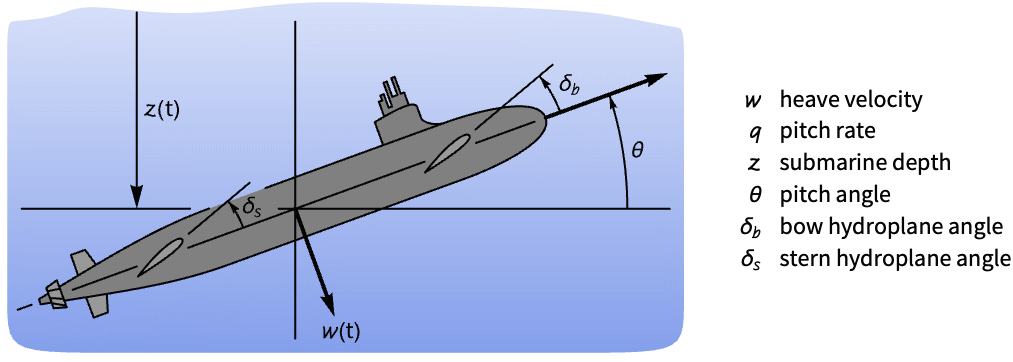
航空宇宙系 (3)
生物学系 (1)
化学系 (1)
電気系 (1)
特性と関係 (5)
DiscreteLQRegulatorGainsは,エミュレートされた離散時間系のゲインとして計算される:
DiscreteLQRegulatorGainsは同じ結果を与える:
サンプリング周期を下げるとサンプルされたデータの系がよりよく近似できる:
さまざまな ![]() の値についての離散時間閉ループ系とフィードバックゲイン:
の値についての離散時間閉ループ系とフィードバックゲイン:
サンプリング周期が短くなるにつれて,系の応答間の相違も小さくなる:
サンプリング周期を短くすると,サンプルデータの系の制御努力の近似がよりよくなる:
サンプリング周期が短くなると,系の制御努力間の違いも小さくなる:
関連するガイド
-
▪
- 状態空間モデルを使った設計 ▪
- 制御系
テキスト
Wolfram Research (2010), DiscreteLQRegulatorGains, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiscreteLQRegulatorGains.html (2021年に更新).
CMS
Wolfram Language. 2010. "DiscreteLQRegulatorGains." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/DiscreteLQRegulatorGains.html.
APA
Wolfram Language. (2010). DiscreteLQRegulatorGains. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteLQRegulatorGains.html
BibTeX
@misc{reference.wolfram_2025_discretelqregulatorgains, author="Wolfram Research", title="{DiscreteLQRegulatorGains}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteLQRegulatorGains.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_discretelqregulatorgains, organization={Wolfram Research}, title={DiscreteLQRegulatorGains}, year={2021}, url={https://reference.wolfram.com/language/ref/DiscreteLQRegulatorGains.html}, note=[Accessed: 06-February-2026]}