DiscreteLQRegulatorGains
DiscreteLQRegulatorGains[sspec,wts,τ]
给出离散时间状态反馈增益矩阵,其中,对于最小化权重为 wts 的成本函数的连续时间系统指定 sspec,采样周期为 τ.
DiscreteLQRegulatorGains[…,"prop"]
给出属性 "prop" 的值.
更多信息和选项

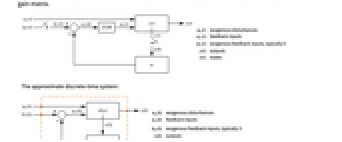

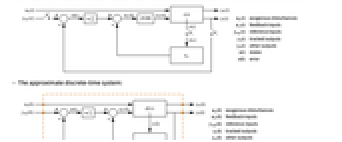
- DiscreteLQRegulatorGains 亦称为离散线性二次调节器、离散线性二次成本等效调节器或离散线性二次仿真调节器.
- DiscreteLQRegulatorGains 通常用于计算调节控制器或跟踪控制器的数字化实现.
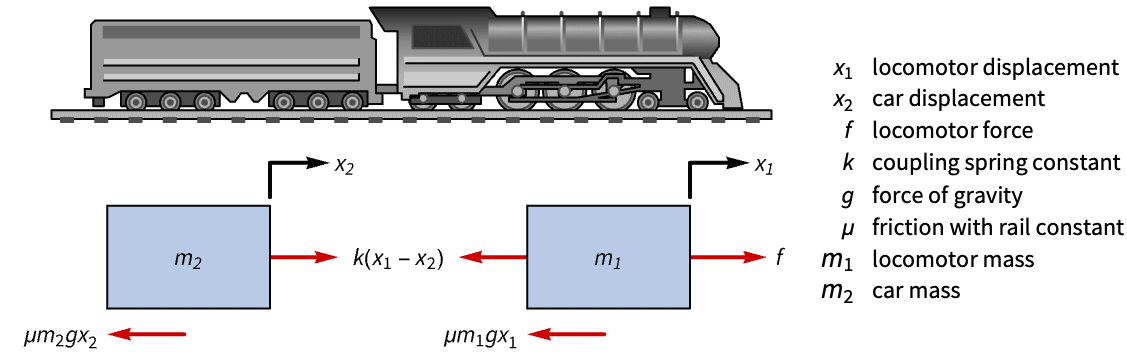
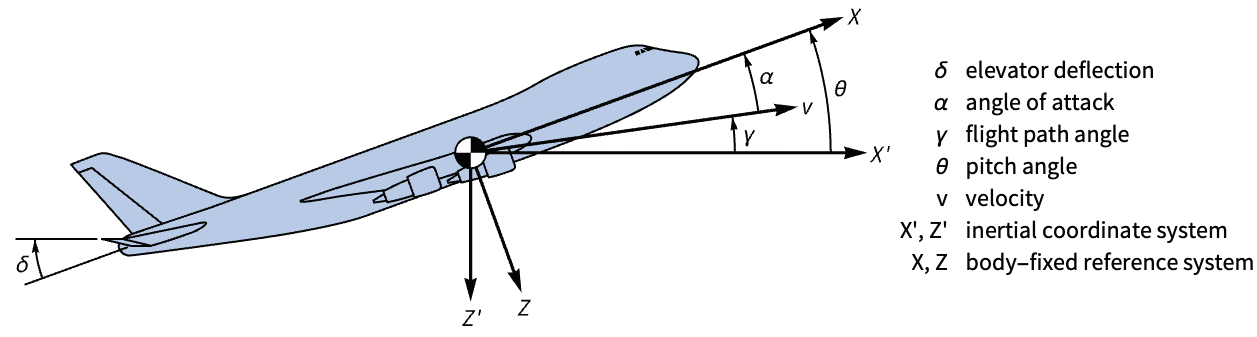
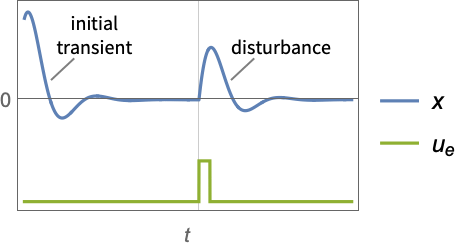
- 调节控制器旨在尽管有
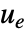 干扰的情况下仍将系统保持在平衡状态. 典型范例包括将倒立摆保持在直立位置或保持飞机水平飞行.
干扰的情况下仍将系统保持在平衡状态. 典型范例包括将倒立摆保持在直立位置或保持飞机水平飞行. - 调节控制器由
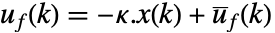 的控制律给出,其中
的控制律给出,其中 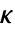 是计算得到的增益矩阵.
是计算得到的增益矩阵. - 连续时间成本函数由
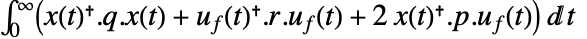 给出.
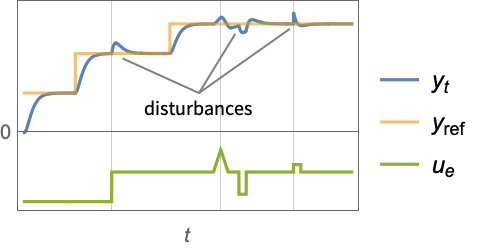
给出. - 跟踪控制器旨在有扰动
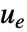 干扰的情况下跟踪参考信号. 典型范例包括汽车的巡航控制系统或机器人的路径跟踪.
干扰的情况下跟踪参考信号. 典型范例包括汽车的巡航控制系统或机器人的路径跟踪. - 跟踪控制器由形式为
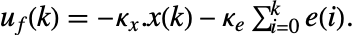 的控制律给出,其中
的控制律给出,其中 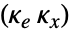 是计算出的增强系统的增益矩阵,包括系统 sys 和
是计算出的增强系统的增益矩阵,包括系统 sys 和 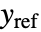 的动力.
的动力. - 近似离散时间系统:
- 连续时间成本函数由
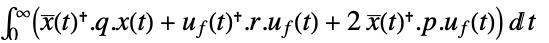 给出,其中
给出,其中 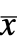 为增强状态.
为增强状态. - 增强状态的数量由
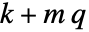 给出,其中
给出,其中 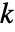 由 sys 的 SystemsModelOrder 给出、
由 sys 的 SystemsModelOrder 给出、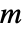 由 yref 的阶给出、
由 yref 的阶给出、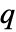 由 yref 的信号数给出.
由 yref 的信号数给出. - 权重矩阵的选择需要性能和控制工作量之间的平衡,通过迭代可以获取比较理想的设计. 它们的起始值可以是有项
![TemplateBox[{{1, /, z}, i, 2}, Subsuperscript] TemplateBox[{{1, /, z}, i, 2}, Subsuperscript]](Files/DiscreteLQRegulatorGains.zh/21.png) 的对角矩阵,其中 zi 是相应的 xi 或 ui 的最大允许绝对值.
的对角矩阵,其中 zi 是相应的 xi 或 ui 的最大允许绝对值. - DiscreteLQRegulatorGains 使用连续时间成本函数的近似离散时间等效值计算离散时间控制器.
- 离散时间近似成本函数是
![sum_(k=0)^infty(x^^(k).phi.x^^(k)+TemplateBox[{{{u, _, f}, (, k, )}}, ConjugateTranspose].rho.u_f(k)+2 TemplateBox[{{{x, ^, ^}, (, k, )}}, ConjugateTranspose].psi.u_f(k)) sum_(k=0)^infty(x^^(k).phi.x^^(k)+TemplateBox[{{{u, _, f}, (, k, )}}, ConjugateTranspose].rho.u_f(k)+2 TemplateBox[{{{x, ^, ^}, (, k, )}}, ConjugateTranspose].psi.u_f(k))](Files/DiscreteLQRegulatorGains.zh/22.png) ,具有以下项:
,具有以下项: -
状态权重矩阵 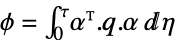
输入权重矩阵 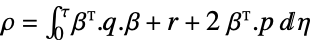
交叉耦合权重矩阵 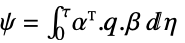
状态向量 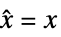 用于调节且
用于调节且 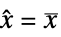 用于追踪
用于追踪 - 权重 wts 可采用以下形式:
-
{q,r} 没有交叉耦合的成本函数 {q,r,p} 含有交叉耦合矩阵 p 的成本函数 - 系统规约 sspec 是系统 sys 与 uf、yt 和 yref 规约.
- 系统 sys 可以 StateSpaceModel[{a,b,c,d}] 形式给出,其中 a, b, c 和 d 分别表示状态、输入、输出和连续时间系统中的馈通矩阵
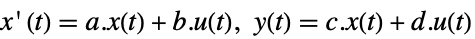 .
. - 离散时间设计模型 dsys 为保持零阶的近似形式
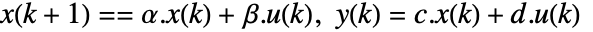 ,有如下项:
,有如下项: -
状态矩阵 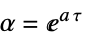
输入矩阵 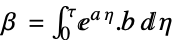
- 系统指定 sspec 可采用以下形式:
-
StateSpaceModel[…] 线性控制输入和线性状态 AffineStateSpaceModel[…] 线性控制输入和非线性状态 NonlinearStateSpaceModel[…] 非线性控制输入和非线性状态 SystemModel[…] 一般系统模型 <…> 用 Association 给出的详细系统指定 - 详细系统指定中可含有以下键:
-
"InputModel" sys 任意一个模型 "FeedbackInputs" All 反馈输入 uf "TrackedOutputs" None 跟踪输出 yt "TrackedSignal" Automatic yref 的动力 - 反馈输入可采用以下形式:
-
{num1,…,numn} 由 StateSpaceModel、AffineStateSpaceModel 和 NonlinearStateSpaceModel 使用的编号输入 numi {name1,…,namen} 由 SystemModel 使用的编号输入 namei All 使用所有输入 - 对于非线性系统,如 AffineStateSpaceModel、NonlinearStateSpaceModel 和 SystemModel,系统将围绕其存储的工作点进行线性化.
- DiscreteLQRegulatorGains[…,"Data"] 返回一个 SystemsModelControllerData 对象 cd,可通过 cd["prop"] 提取其他属性.
- 可用 DiscreteLQRegulatorGains[…,"prop"] 直接给出 cd["prop"] 的值.
- 属性 "prop" 可取的值包括:
-
"Design" 控制器设计的类型 "DesignModel" 设计所用的模型 "DiscreteTimeClosedLoopPoles" "DiscreteTimeClosedLoopSystem" 的极点 "DiscreteTimeClosedLoopSystem" dcsys {"DiscreteTimeClosedLoopSystem",cspec} 是否合并离散时间闭环系统 "DiscreteTimeControllerModel" dcm "DiscreteTimeDesignModel" 近似离散时间模型 dsys "DiscreteTimeOpenLoopPoles" dsys 的极点 "DiscreteTimeWeights" 近似成本函数的权重 ϕ、ρ、π "FeedbackGains" 增益矩阵 κ 或其等价物 "DiscreteTimeFeedbackGainsModel" dgm or {dgm1,dgm2} "FeedbackInputs" 用 sys 的 uf 作为反馈 "InputModel" 输入模型 sys "InputsCount" sys 的输出 y 的个数 "OpenLoopPoles" "DesignModel" 的极点 "OutputsCount" sys 的输出 y 的个数 "SamplingPeriod" 采样 period τ "StatesCount" sys 的状态 x 的数量 "TrackedOutputs" 被跟踪的 sys 的输出 yt - cspec 的密钥包括:
-
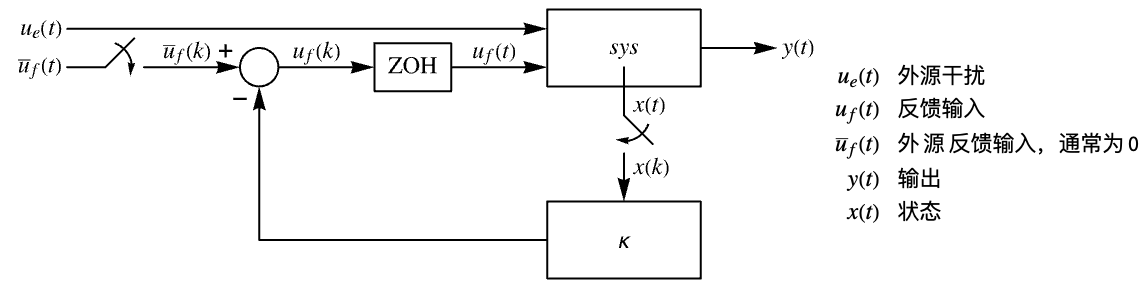
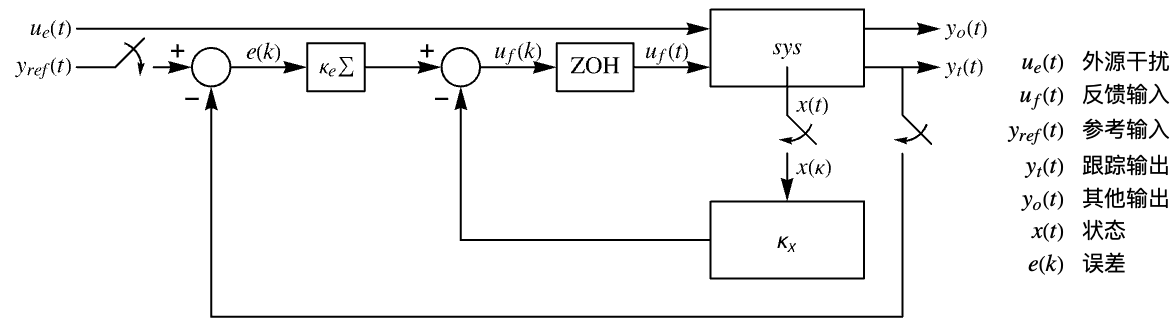
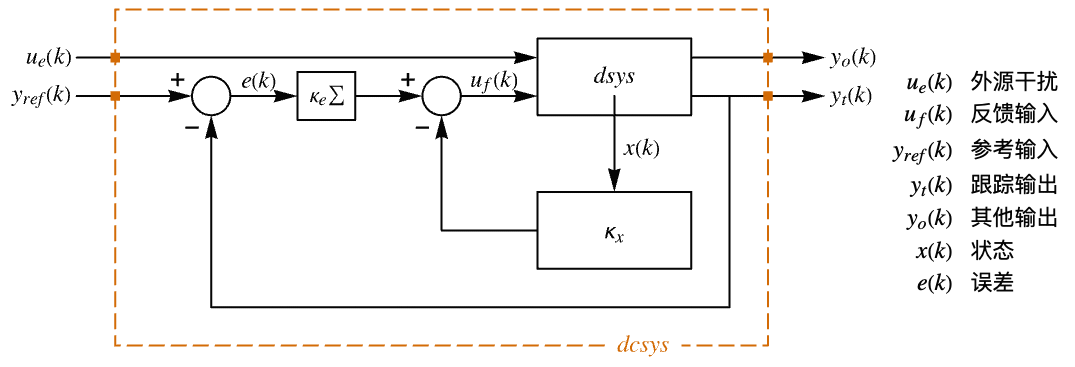
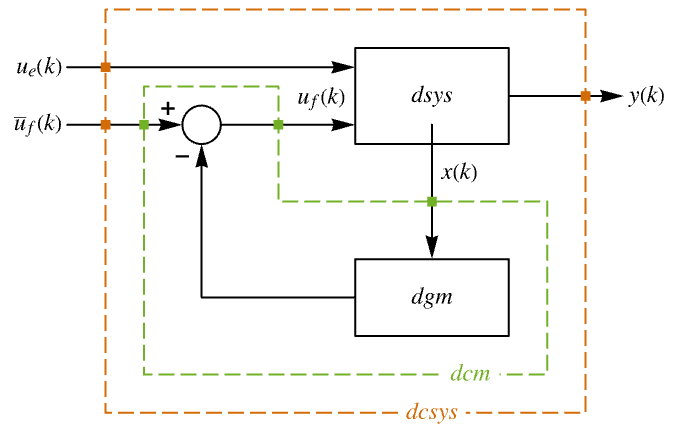
"InputModel" csys 中的输入模型 "Merge" 是否合并 csys "ModelName" csys 的名称 - 近似离散时间调节器布局图.
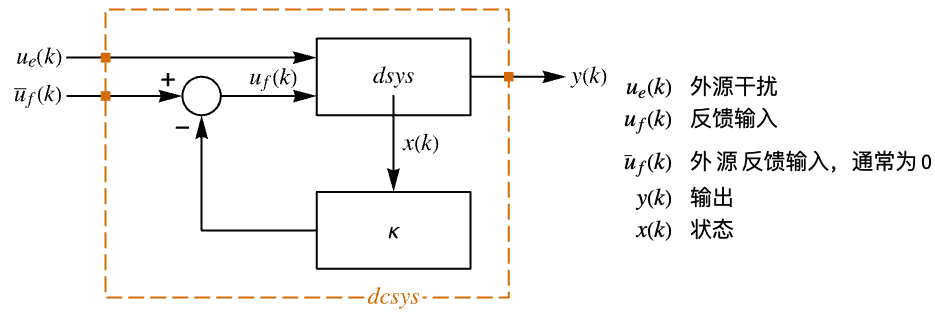
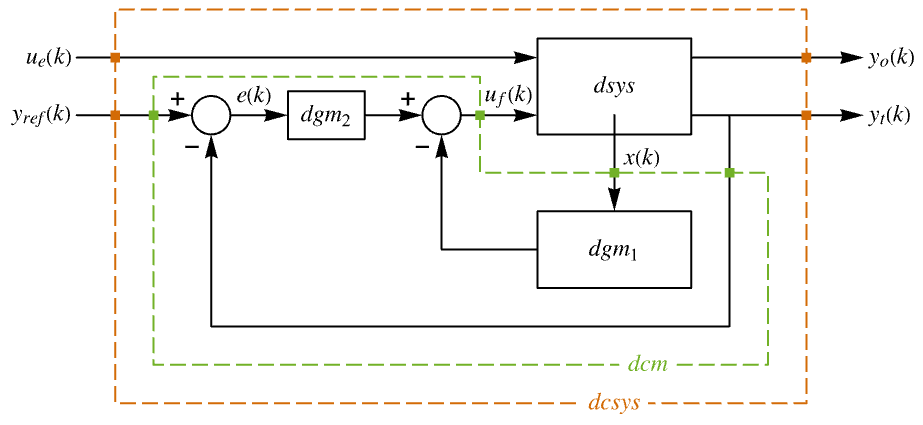
- 近似离散时间跟踪器布局图.
范例
打开所有单元关闭所有单元基本范例 (4)
范围 (26)
基本用法 (7)
工厂模型 (5)
跟踪 (3)
应用 (12)
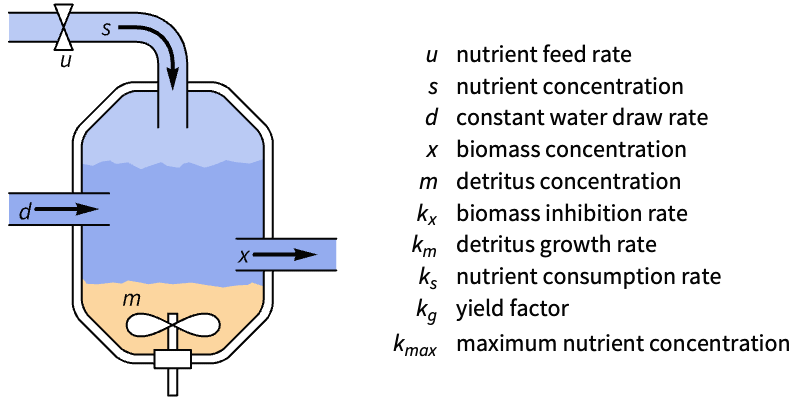
生物系统 (1)
使用 StateSpaceModel 线性化系统:
化学系统 (1)
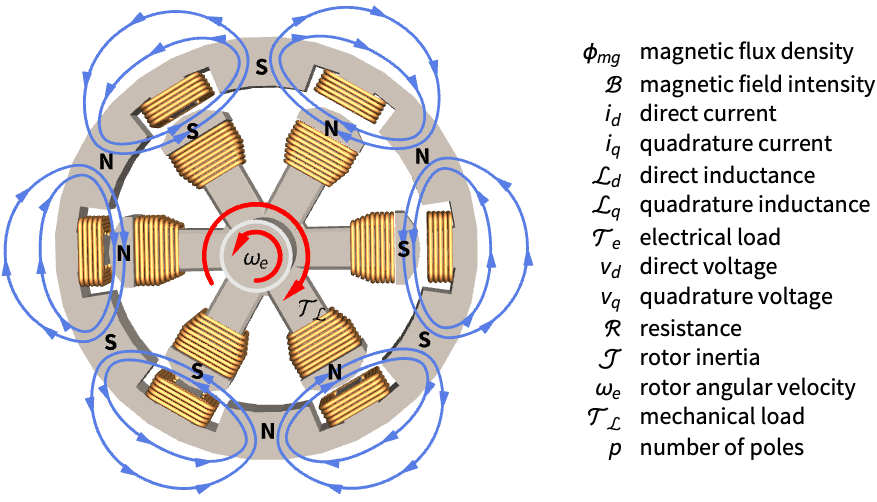
电气系统 (1)
属性和关系 (5)
DiscreteLQRegulatorGains 计算为仿真离散时间系统的增益:
DiscreteLQRegulatorGains 给出相同的结果:
Wolfram Research (2010),DiscreteLQRegulatorGains,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteLQRegulatorGains.html (更新于 2021 年).
文本
Wolfram Research (2010),DiscreteLQRegulatorGains,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteLQRegulatorGains.html (更新于 2021 年).
CMS
Wolfram 语言. 2010. "DiscreteLQRegulatorGains." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/DiscreteLQRegulatorGains.html.
APA
Wolfram 语言. (2010). DiscreteLQRegulatorGains. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiscreteLQRegulatorGains.html 年