DiscreteRiccatiSolve

DiscreteRiccatiSolve[{a,b},{q,r}]

離散代数リッカチ(Riccati)方程式 TemplateBox[{a}, ConjugateTranspose].x.a-x-TemplateBox[{a}, ConjugateTranspose].x.b.TemplateBox[{{(, {r, +, {TemplateBox[{b}, ConjugateTranspose], ., x, ., b}}, )}}, Inverse].TemplateBox[{b}, ConjugateTranspose].x.a+q=0の安定化解である行列 を与える．

DiscreteRiccatiSolve[{a,b},{q,r,p}]

TemplateBox[{a}, ConjugateTranspose].x.a-x-(TemplateBox[{a}, ConjugateTranspose].x.b+p).TemplateBox[{{(, {r, +, {TemplateBox[{b}, ConjugateTranspose], ., x, ., b}}, )}}, Inverse].(TemplateBox[{b}, ConjugateTranspose].x.a+TemplateBox[{p}, ConjugateTranspose])+q=0を解く．

詳細とオプション

  • TemplateBox[{a}, ConjugateTranspose].x.a-x-TemplateBox[{a}, ConjugateTranspose].x.b.TemplateBox[{{(, {r, +, {TemplateBox[{b}, ConjugateTranspose], ., x, ., b}}, )}}, Inverse].TemplateBox[{b}, ConjugateTranspose].x.a+q=0における「」は共役転置を表す．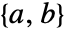
  • が安定可能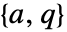，が検出可能で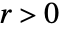，かつ 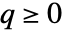のときのみ，方程式 TemplateBox[{a}, ConjugateTranspose].x.a-x-TemplateBox[{a}, ConjugateTranspose].x.b.TemplateBox[{{(, {r, +, {TemplateBox[{b}, ConjugateTranspose], ., x, ., b}}, )}}, Inverse].TemplateBox[{b}, ConjugateTranspose].x.a+q=0 には一意的で対称な半正定値解がある．したがって，行列 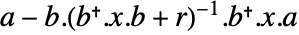の固有値はすべて単位円内にあり解は安定している．
  • が可制御でが可観測であれば解は正定値である．
  • DiscreteRiccatiSolveはMethodオプションをサポートする．次は，指定可能な設定値である．
  • Automatic自動的に決定されたメソッド
    "Eigensystem"固有値分解に基づく
    "GeneralizedEigensystem"一般化された固有値分解に基づく
    "GeneralizedSchur"一般化されたシューア(Schur)分解に基づく
    "InverseFree""GeneralizedSchur"の変化形
    "MatrixSign"行列符号関数を使った反復法
    "Newton"反復ニュートン(Newton)法
    "Schur"シューア分解に基づく
  • どのメソッドも，近似数値行列に適用される．"Eigensystem"は厳密行列に適用される．

例題

すべて開くすべて閉じる

例  (1)

離散代数リッカチ方程式を解く：

解を確かめる：

スコープ  (3)

離散リッカチ方程式を解く：

クロスカップリング行列を含む離散リッカチ方程式を解く：

サンプルデータの伝達関数モデルのリッカチ方程式を解く：

オプション  (7)

Method  (7)

厳密な系には，Automaticおよび"Eigensystem"メソッドが使われる：

厳密ではない系にも用いられる：

厳密ではない系には"Schur"メソッドを使うことができる：

"Newton"は非厳密系に適用され，Automaticよりも正確な場合がある：

解と絶対誤差を計算する：

デフォルトのメソッドと比較する：

"Newton"は，サブオプションとして，"StartingMatrix"，"MaxIterations"，"Tolerance"を取る：

"Newton"法は，たとえそれが存在する場合でも，安定化解を計算しないことがある：

Automaticメソッドと比較する：

"MatrixSign"は，一般に，"Newton"法の初期近似として使われる：

xinitを使って"Newton"法を初期化する：

誤差を比較する：

"MatrixSign"は，サブオプションとして，"MaxIterations"および"Tolerance"を取る：

a が特異値の場合は，"GeneralizedSchur"あるいは"GeneralizedEigensystem"が適用される：

行列 a は特異行列である：

これら2つのメソッドは，特異行列 a に使うことができる：

誤差を確かめる：

"Eigensystem"は，a が特異行列のときは使うことができない：

"InverseFree"は，r の条件がよくない場合に使うことができる：

行列 r の条件番号は高い：

このメソッドを使う：

デフォルトのメソッドと比較する：

この場合は，デフォルトメソッドの方が絶対誤差が大きい：

アプリケーション  (2)

線形化されたターボ発電機モデルには状態と入力の行列がある：

指定された重み行列{q,r}および初期状態 s0についての離散線形二次調整器費用 Jopt：

すべての閉ループ極が半径 の円内にあることを保証する最適状態フィードバックゲインを計算する：

規定の安定度を持たない閉ループの極：

特性と関係  (10)

DiscreteRiccatiSolve[{a,b},{q,r,p}]はDiscreteRiccatiSolve[{a-b.r^( -1).p,b},{q-p.r -1.p,r}]に等しい：

p を行列 a および q に組み込んでも同じ結果を得ることができる：

{a,b}が安定化可能，{a,g}が検出可能で q=Transpose[g].g であれば，離散リッカチ方程式の解は半正定値である：

{a,b}が可制御で{a,g}が可観測であり q=Transpose[g].g であれば，離散リッカチ方程式の解は正定値である：

離散代数リッカチ方程式に関連する行列はシンプレクティックである：

シンプレクティック行列の固有値は の形のペアである：

と は相似行列である：

リッカチ方程式の安定化解を得るためには，シンプレクティック行列は安定性および相補性の特性を満足しなければならない：

安定性特性：

相補性特性：

安定化解：

のあるフィードバック系の固有値はシンプレクティック行列の安定固有値である：

DiscreteRiccatiSolveを使って最適状態フィードバックゲインを計算する：

LQRegulatorGainsを使って同じ結果を直接得る：

DiscreteRiccatiSolveを使って最適出力フィードバックゲインを計算する：

LQOutputRegulatorGainsは同じ結果を与える：

DiscreteRiccatiSolveを使って最適推定器ゲインを計算する：

LQEstimatorGainsを使う：

系の離散近似の最適軌道は高くつく：

s0から始まる系の最適線形二次調整器費用：

考えられる問題  (1)

{a,b}が安定化不可能で{a,g}が検出不可能であれば，q=g.g のリッカチ方程式には安定化解がない：

Wolfram Research (2010), DiscreteRiccatiSolve, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiscreteRiccatiSolve.html （2014年に更新）.

テキスト

Wolfram Research (2010), DiscreteRiccatiSolve, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiscreteRiccatiSolve.html （2014年に更新）.

CMS

Wolfram Language. 2010. "DiscreteRiccatiSolve." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/DiscreteRiccatiSolve.html.

APA

Wolfram Language. (2010). DiscreteRiccatiSolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteRiccatiSolve.html

BibTeX

@misc{reference.wolfram_2024_discretericcatisolve, author="Wolfram Research", title="{DiscreteRiccatiSolve}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteRiccatiSolve.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_discretericcatisolve, organization={Wolfram Research}, title={DiscreteRiccatiSolve}, year={2014}, url={https://reference.wolfram.com/language/ref/DiscreteRiccatiSolve.html}, note=[Accessed: 21-November-2024 ]}