DiscreteVariables
是 NDSolve 和其他函数的一个选项,指定只在时间积分中离散时间发生改变的变量.
更多信息

- DiscreteVariables->{v1, v2,…} 指定 v1、v2、… 应该被视为只在离散时间发生改变的变量.
- 离散变量 v 的值可以通过 WhenEvent[event,v->val] 或者 WhenEvent[event,v->"DiscontinuitySignature"] 改变.
- 离散变量解 v 可以通过使用 NDSolve[eqn,{v,…},…] 返回.
- DiscreteVariables->{vspec1,vspec2,…} 可用于指定离散变量的范围.
- vspeci 的可能形式是:
-
v v 具有范围 Reals 或者 Complexes Element[v,Reals] v 具有范围 Reals Element[v,Complexes] v 具有范围 Complexes Element[v,Integers] v 具有范围 Integers Element[v,{n1,…}] v 具有离散范围 {n1,…} {v,vmin,vmax} v 具有范围 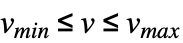
vspeciactioni 执行 actioni 当不再满足 vspeci 时 - 几乎所有地方,关于时间的离散变量的导数都是零,并且不应该出现在方程中.
- 对于偏微分方程,在线半离散化方法中,离散变量只取决于时间自变量.
范例
打开所有单元关闭所有单元范围 (7)
应用 (5)
Wolfram Research (2012),DiscreteVariables,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteVariables.html.
文本
Wolfram Research (2012),DiscreteVariables,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteVariables.html.
CMS
Wolfram 语言. 2012. "DiscreteVariables." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteVariables.html.
APA
Wolfram 语言. (2012). DiscreteVariables. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiscreteVariables.html 年