FindHamiltonianPath

FindHamiltonianPath[g]

グラフ g 中の最短のハミルトン(Hamilton)路を求める．

FindHamiltonianPath[g,s,t]

s から t までの最短のハミルトン路を求める．

詳細とオプション

  • FindHamiltonianPathは，ハミルトン路問題としても知られている．
  • ハミルトン路は各頂点を厳密に1度訪れる．
  • FindHamiltonianPathは，ハミルトン路が存在しない場合はリスト{}を返す．

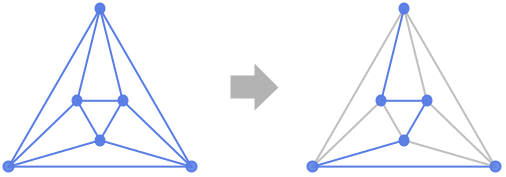
例題

すべて開くすべて閉じる

例  (1)

グラフ中の頂点を通るハミルトン路を求める：

経路をハイライトする：

グラフ中の2つの別々の頂点間のハミルトン路を求める：

経路をハイライトする：

スコープ  (3)

FindHamiltonianPathは無向グラフに使うことができる：

重み付きグラフ：

FindHamiltonianPathは大きいグラフに使うことができる：

オプション  (1)

DistanceFunction  (1)

次は，6点間の疎な距離行列を定義する：

ハミルトン路を求める：

経路をハイライトする：

アプリケーション  (2)

8×8のチェス盤上で，各正方形を厳密に1度訪れるチェスの駒のナイトの連続する動きを求める：

ナイトの動き：

ヨーロッパのギリシャからドイツまでのハミルトン路を求める：

地理的中心の経緯度：

ヨーロッパの重み付きグラフを構築する：

ツアーを示す：

特性と関係  (2)

ハミルトン路を含むグラフがハミルトン閉路を含まないことがある：

ハミルトン閉路を含むグラフはハミルトン路を含む：

Wolfram Research (2015), FindHamiltonianPath, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindHamiltonianPath.html.

テキスト

Wolfram Research (2015), FindHamiltonianPath, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindHamiltonianPath.html.

CMS

Wolfram Language. 2015. "FindHamiltonianPath." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FindHamiltonianPath.html.

APA

Wolfram Language. (2015). FindHamiltonianPath. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindHamiltonianPath.html

BibTeX

@misc{reference.wolfram_2024_findhamiltonianpath, author="Wolfram Research", title="{FindHamiltonianPath}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FindHamiltonianPath.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findhamiltonianpath, organization={Wolfram Research}, title={FindHamiltonianPath}, year={2015}, url={https://reference.wolfram.com/language/ref/FindHamiltonianPath.html}, note=[Accessed: 14-November-2024 ]}