FindMatrixGameStrategies[mgame]
MatrixGame mgame の最適な戦略プロファイル(ナッシュ均衡)を求める.
FindMatrixGameStrategies[mgame,spec]
指定 spec に従って戦略プロファイルを求める.


FindMatrixGameStrategies
FindMatrixGameStrategies[mgame]
MatrixGame mgame の最適な戦略プロファイル(ナッシュ均衡)を求める.
FindMatrixGameStrategies[mgame,spec]
指定 spec に従って戦略プロファイルを求める.
詳細とオプション

- FindMatrixGameStrategiesは,ゲームの解法あるいはナッシュ均衡のようなゲームの最適戦略を求めることとしても知られている.
- 最適なゲーム戦略は,通常,ゲームの戦い方として,あるいはゲームを行うことから得られる期待利得の計算に使われる.
- FindMatrixGameStrategiesはゲーム戦略のリストを返す.
- 全プレーヤーが同時に利得を最大化するなら,戦略プロファイル
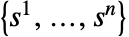 はナッシュ均衡である.同様に,どのプレーヤーも戦略を変更することで期待される利益を向上させることはできない.
はナッシュ均衡である.同様に,どのプレーヤーも戦略を変更することで期待される利益を向上させることはできない. - 戦略プロファイルは
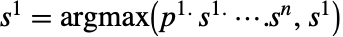 , …,
, …, 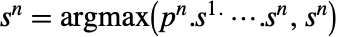 で与えられる.ここで,各最大化は戦略
で与えられる.ここで,各最大化は戦略 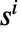 を確率ベクトルとして取る.
を確率ベクトルとして取る. - どの行列ゲームも,通常は多数の,混合戦略の形のナッシュ均衡を持つ,
- 次は,spec の可能な指定方法である.
-
"Mixed" 行動の確率混合 "Pure" 単一の行動 - FindMatrixGameStrategiesには次のオプションがある.
-
Method "SolveValues" 使用するメソッド - 次は,可能なMethod設定である.
-
"FindInstance" 整方程式にFindInstanceを使う {"FindInstance",n} 整方程式の 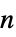 個の解を求める
個の解を求める"NSolveValues" 整方程式にNSolveValuesを使う "SolveValues" 整方程式にSolveValuesを使う
例題
すべて開く すべて閉じる例 (5)
スコープ (5)
オプション (1)
Method (1)
アプリケーション (8)
社会ゲーム (2)
ボランティアのジレンマは,各プレーヤーがボランティア活動に参加することもしないこともできる環境を表している.少なくとも1人のプレーヤーがボランティア活動に参加すると他のすべてのプレーヤーは参加しないことによってわずかに得をする.誰も参加しないとすべてのプレーヤーの利得が低くなる.プレーヤーが4人のボランティアのジレンマゲームを生成する:
ボランティアのジレンマは,多くの場合ナッシュ均衡が存在し,厳密に1人のプレーヤーが活動に参加する可能性が最も高くなる.このゲームに最適な戦略を求める:
非調整ゲームは調整ゲームと反調整ゲームのハイブリッド形式で,片方のプレーヤーのインセンティブが調整することであるのに対しもう一方のプレーヤーはこれを回避しようとする.1人の志願者と1人の反対者からなる非調整ゲームを生成する:
経済ゲーム (3)
腹をすかせた3人の男がレストランに行く.支払いは割り勘にすることにした.レストランには3種類の定食(安い,普通,高い)がある.この状況をMatrixGameとして表す:
Cournot寡占ゲームは複数の企業が同じ製品を製造している状況を表している.各企業は製造コストと他の企業の製品製造数を考慮しなければならない.最低価格の企業だけが商品を販売することができる.Cournot寡占ゲームを生成する:
すべてのプレーヤーを考慮すると,利得は2番目の行動で最大になると直感的に分かる:
価格戦争は,複数の企業が最低価格を提供しようとするが任意の企業の利得が選択される価格に直接相関することである.3つの企業間の価格戦争について考える.各企業は低価格か高価格を選ぶことができる:
軍事ゲーム (1)
関連するガイド
-
▪
- ゲーム理論
テキスト
Wolfram Research (2025), FindMatrixGameStrategies, Wolfram言語関数, https://reference.wolfram.com/language/ref/FindMatrixGameStrategies.html.
CMS
Wolfram Language. 2025. "FindMatrixGameStrategies." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FindMatrixGameStrategies.html.
APA
Wolfram Language. (2025). FindMatrixGameStrategies. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindMatrixGameStrategies.html
BibTeX
@misc{reference.wolfram_2025_findmatrixgamestrategies, author="Wolfram Research", title="{FindMatrixGameStrategies}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/FindMatrixGameStrategies.html}", note=[Accessed: 11-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_findmatrixgamestrategies, organization={Wolfram Research}, title={FindMatrixGameStrategies}, year={2025}, url={https://reference.wolfram.com/language/ref/FindMatrixGameStrategies.html}, note=[Accessed: 11-February-2026]}